
Modification of the LS-STAG Immersed Boundary Method for Simulating Turbulent Flows
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
23
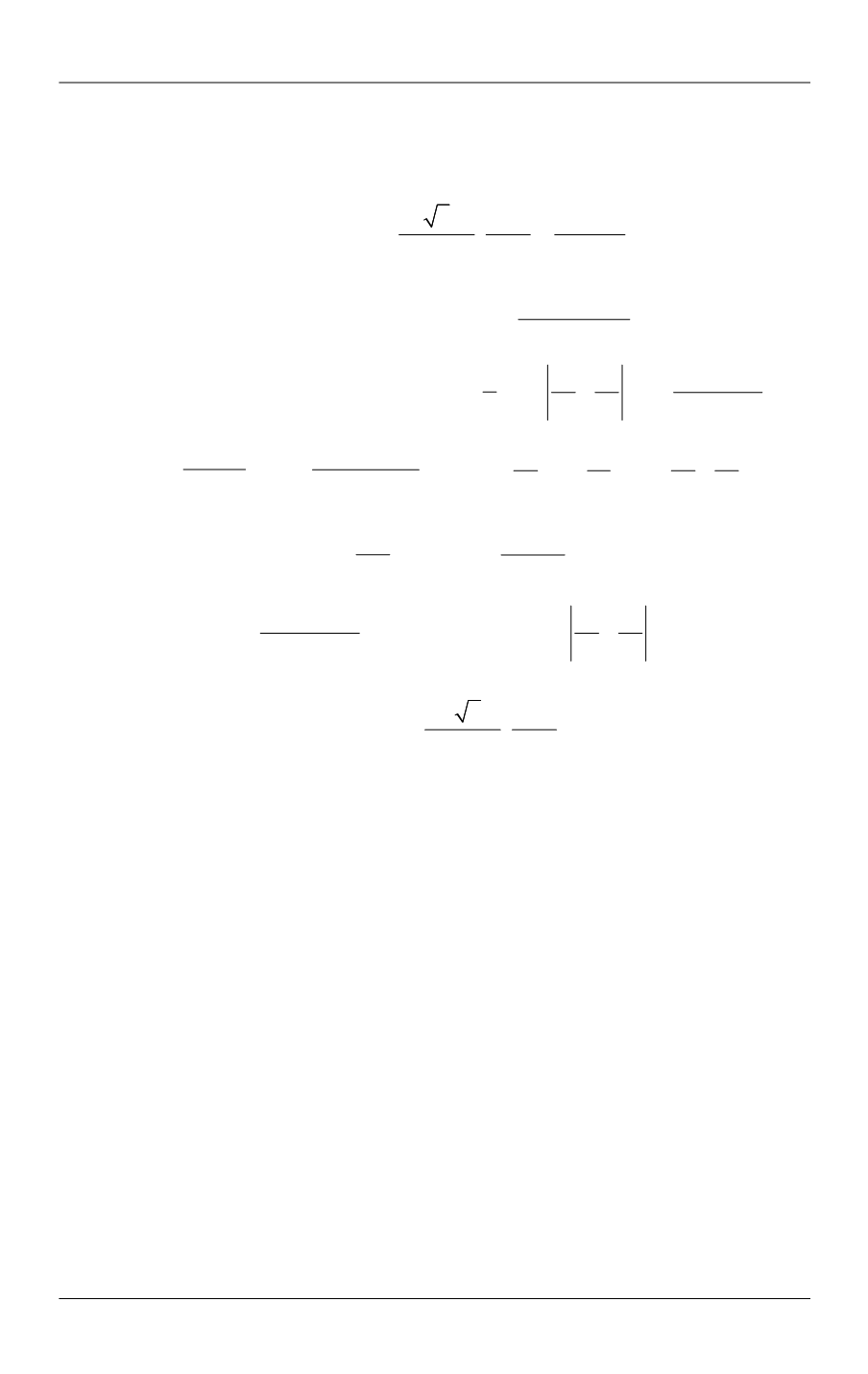
The following designations are introduced in Table 2:
is the Spalart —
Allmaras (S-A) working variable [4];
is the dissipation rate of the turbulent kinetic
energy
;
k
is the specific dissipation rate of
;
k
4
1
2
2
500 3.424
= tanh min max
,
,
;
0.09
w w
k w
k
k
F
d d CD d
20
= max( ,10 );
k
k
CD
D
1.712 =
;
k
k
D
2
= 0.1355[1 ] ;
t
P
f S
2 0.5
2
=1.2
;
t
f
e
= ;
2
2
=
;
0.1681
turb
u v
S
f
y x
l
2
1
=1
;
1
f
f
3
1 3
=
;
357.911
f
=
;
t
t
t
xx
yy
xy
u
v
u v
P
x
y
y x
2
2
= 3.2391 0.8061
;
w
t
turb
D
f
f
l
1/6
6
65
=
;
64
w
f
g
g
6
= 0.3(
);
g r
r r
2
= min
,10 ;
0.1681
turb
r
Sl
1
2
= max 0.31 ,
;
u v
G
F
y x
2
2
2
2
500
= tanh max
,
.
0.09
w w
k
F
d d
Modification of the LS-STAG immersed boundary method.
The Cartesian
mesh with cells
,
1
1
=( , ) ( ,
)
i j
i
i
j
j
x x y y
is introduced in the rectangular
computational domain
.
It is denoted that
,
i j
is the face of
,
i j
cell and
,
= ( , )
c
c c
i
i j
j
x y
x
is the center of this cell, which is called "base mesh". Pressure is
computed in the center of
,
.
i j
Unknown components
,
i j
u
and
,
i j
v
of velocity vector
v
are computed in the middle of fluid parts of the cell faces. These points are
the centers of control volumes
1
1
,
= ( ,
) ( ,
)
u
c c
j
j
i
i
i j
x x
y y
(
x
-mesh) and
,
=
v
i j
1
1
( ,
) ( ,
)
c c
i
i
j
j
x x y y
(
y
-mesh) with faces
,
u
i j
and
,
v
i j
and squares
x
ij
M
and
,
,
y
i j
M
respectively (Fig. 2).
The level-set function
= ( ) = ( , )
x y
r
[9] is used for immersed boundary
ib
description [2]:
( ) < 0,
= \ {
};
( ) = 0,
;
( ) > 0,
.
f
ib
ib
ib
ib
r
r
r
r
r
r
















