
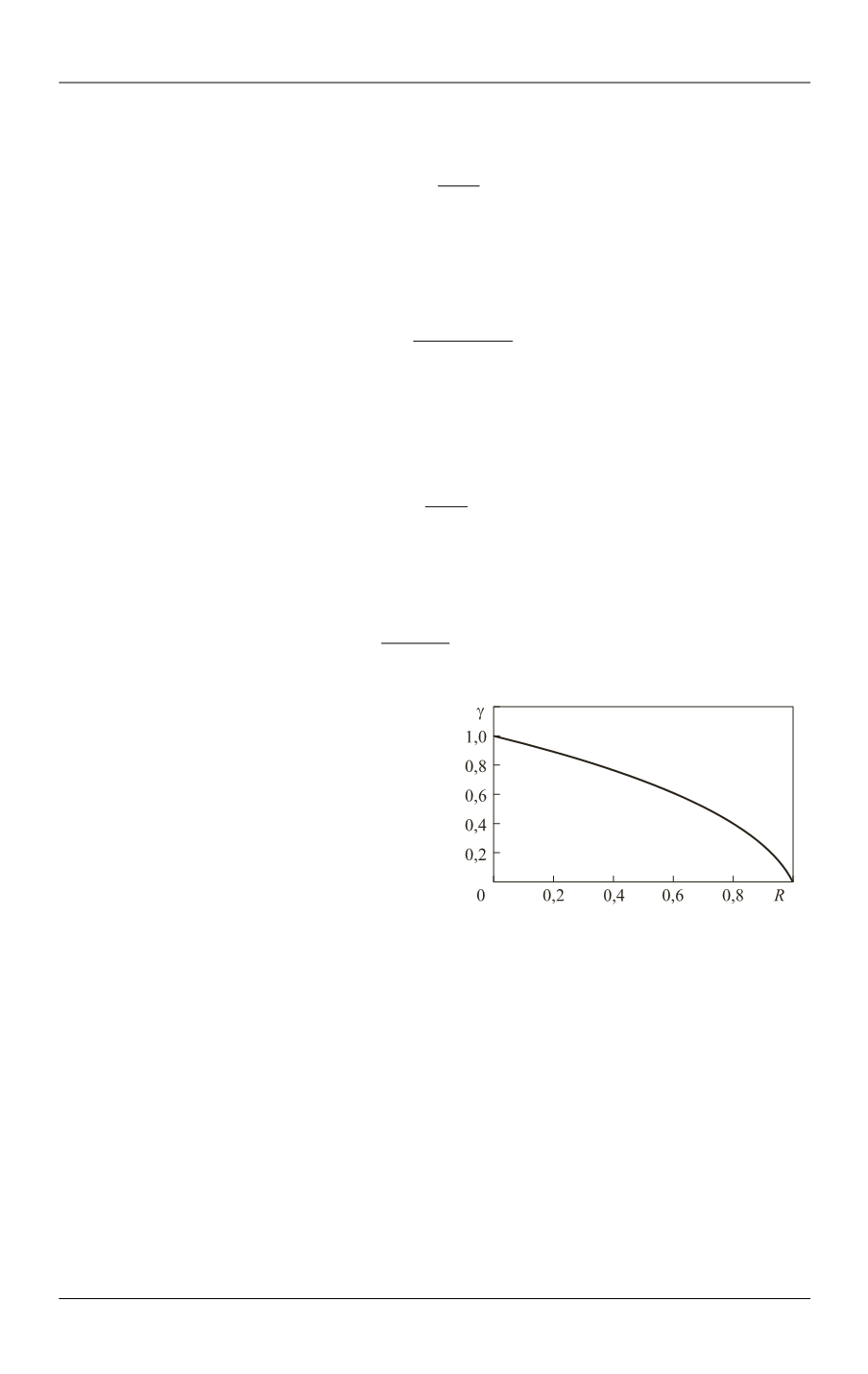
A New Look at Fundamentals of the Photometric Light Transport and Scattering Theory
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
91
Starting from the second term of the series, the trivial infinitely decreasing
geometrical progression is evident. Therefore, the limit for Eq. (33) is:
2 (2)
.
1
s
R
P
R
(34)
Repeating calculations for
N
= 3, 4, 5,… It is easy to find the general probability
P
s
(
N
)
as the solution of our task for the backscattered radiation at MSA inside Δ
x
. It has the
form:
( )
.
1 ( 1)
s
NR
P N
N R
(35)
Substituting
Δx
into the Eq. (27) instead of
H
0
, substituting
,
N x
and equating
(27) and (35), it is easy to derive the scattering coefficient definition at perfect MSA
inside Δ
x
as follows:
.
1
R S
R
(36)
The difference between Eq. (36) and Eq. (22) is noticeable. It is determined by the fac-
tor
(1 ) ln(1 ),
R
R R
R
(37)
which is presented in Fig. 7.
For a small magnitude of
R
, for
example, for
R
< 0.05, the difference is
not significant, low than 10 %. Turbid
biological tissues, for example, have a
quite low conductivity (imaginary part
of the refractive index) in the waveband
of light.
R
usually is not much than
0.1, therefore the SSA can be acceptable.
However, for biological liquids like
blood, this difference has a considerable
impact on results, so the multiple scattering approach should be applied. It can be
illustrated, for example, by ratios of backscattered fluxes and transmitted fluxes, given
by Eqs. (26) and (27) respectively, if different
S
given by Eq. (22) or Eq. (36) is used
for computation. Both cases are cases of MSA due to the usage of Eqs. (26) and (27) as
solutions, but the first one, with
S
given by Eq. (22), is the case of multiple scattering
in terms of the macro-medium, but with the single scattering inside Δ
x
(case 1), while
the second one, with
S
given by Eq. (36), is the pure multiple scattering outright with
the multiple scattering inside Δ
x
(case
2). Figure 8 illustrates differences between
these two cases. We have to note, that
H
0
affects the result in the same way like
because of their direct product in Eqs. (26) and (27).
Fig. 7.
Difference between scattering
coefficients for perfect MSA and SSA
















