
О.В. Щерица, А.О. Гусев, О.С. Мажорова
130
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
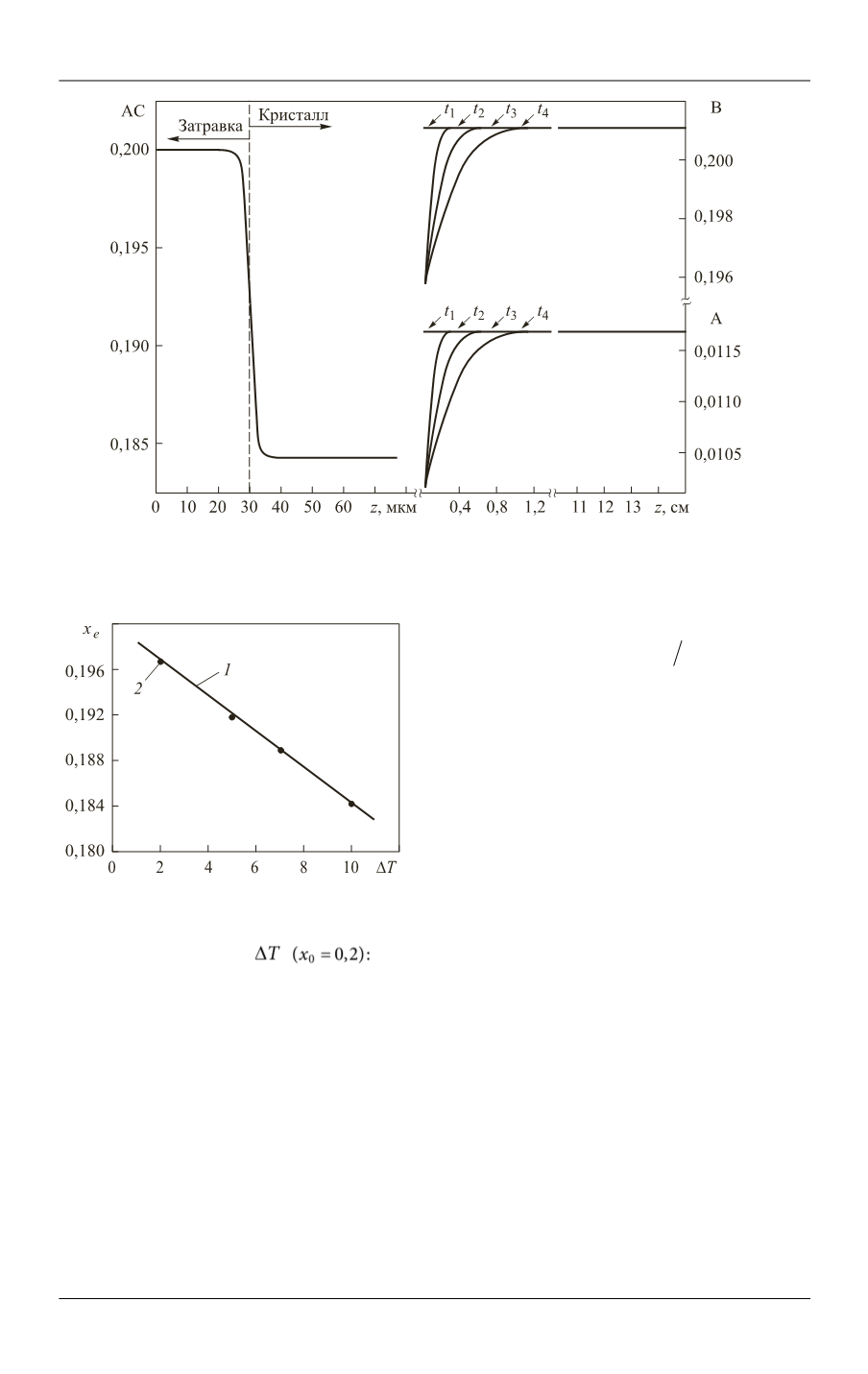
Рис. 2.
Содержание AC в твердой фазе и состав жидкой фазы при изотермическом росте
0
( = 0,2,
x
1
= 0 ,
D
t
t
2
=30 ,
D
t
t
3
=100 ,
D
t
t
4
=300 )
D
t
t
Падение содержания AC на один градус
пересыщения
0
(
)
,
e
x x x T
а также
аппроксимация полученных результатов
линейной функцией представлены на
рис. 3. Мольная доля AC в кристалле убы-
вает с ростом температуры
.
T
Зависи-
мость
e
x
(
T
) с хорошей точностью опи-
сывается функцией
0, 2 0, 0016 ,
e
x
T
что согласуется с данными, приведенными
в работах [20−22].
Отметим следующие достоинства ис-
пользуемого вычислительного алгоритма.
Во-первых, возможность задания на-
чальных данных для расчетов естествен-
ным образом. При изотермическом ре-
жиме выращивания в начальный момент состав расплава не равновесен затрав-
ке, т. е. концентрации веществ в твердой и жидкой фазах не удовлетворяют
уравнениям фазовой диаграммы. Однако для предложенного алгоритма в рас-
смотренном диапазоне параметров не требуется специального согласования
начальных данных, о котором, например, упоминается в работах [7, 23, 24]. Во-
вторых, численный метод является консервативным. Выполнение закона сохра-
нения массы контролировалось на каждом шаге по времени. Масса каждого
компонента оставалась постоянной с точностью, определяемой точностью ре-
шения системы уравнений.
Рис. 3.
Зависимость содержания AC в
выросшем кристалле от степени пере-
сыщения раствора
1
— аппроксимация;
2
— результаты расчета
















