
Об одном методе решения задачи кристаллизации многокомпонентного раствора…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
133
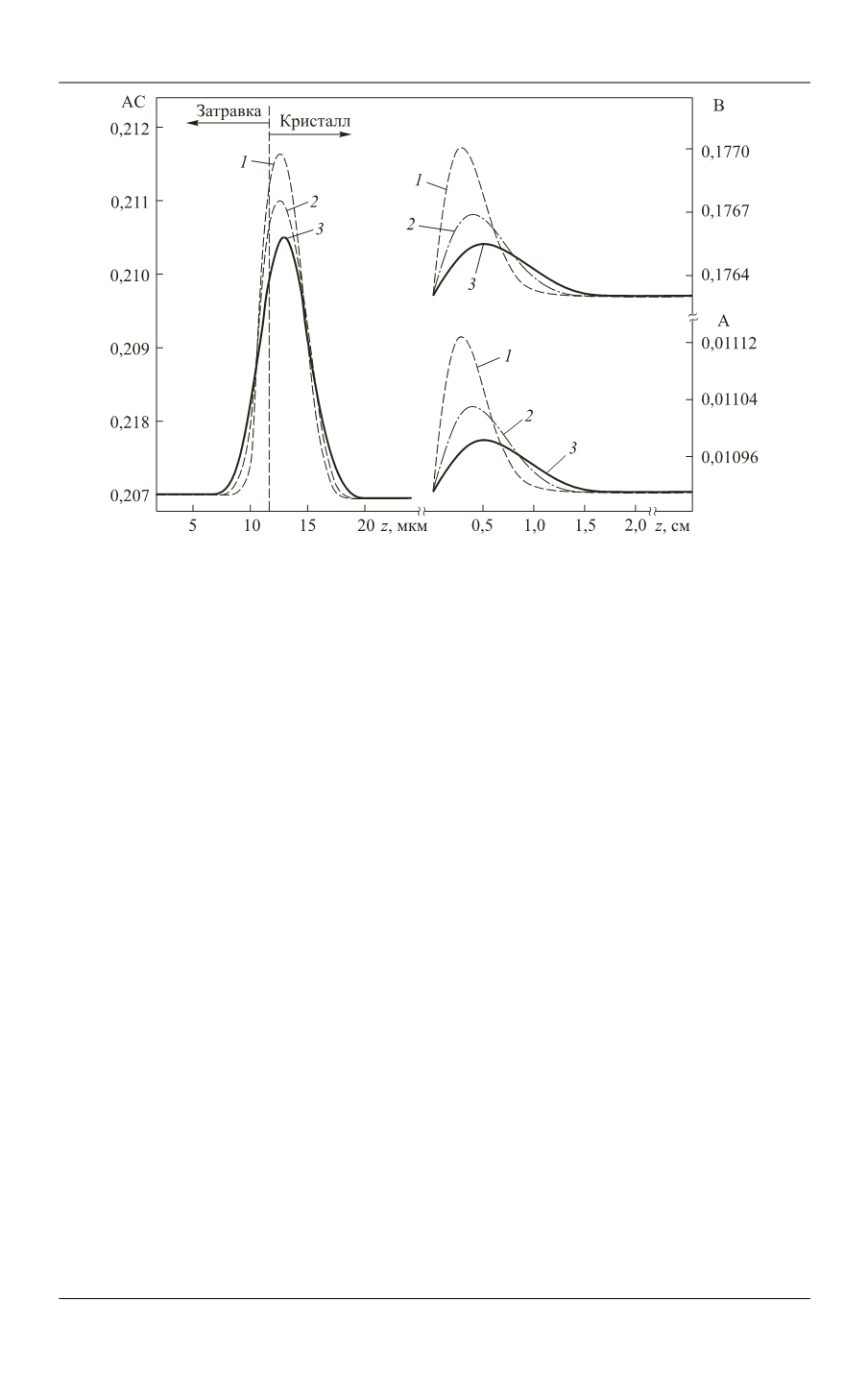
Рис. 7.
Содержание AC в твердой фазе и состав жидкой фазы соединения на этапе роста
эпитаксиального слоя постоянного состава
( =10
T
K,
= 0,5
K/мин,
0
= 0,207)
x
при
t
= 23 (
1
), 35 (
2
) и 52 (
3
) мин
Заключение.
Рассмотрена самосогласованная модель кристаллизации трех-
компонентного раствора в цилиндрической ампуле. Модель учитывает движе-
ние фронта кристаллизации и диффузионный тепломассоперенос в твердой и
жидкой фазах. Предложен метод решения термодиффузионной задачи Стефана,
основанный на совместном решении системы уравнений, описывающей про-
цессы тепломассопереноса и движение фронта кристаллизации. В результате
использования неявной разностной схемы и совместного решения уравнений с
помощью метода Ньютона, построенный метод обладает значительным запасом
устойчивости и гарантирует получение надежных результатов для широкого
класса фазовых диаграмм. Консервативные свойства алгоритма позволяют про-
водить численное моделирование режимов смены растворения ростом. Пред-
ложенный метод применялся для решения задачи о кристаллизации трехком-
понентного раствора, однако он очевидным образом обобщается на случай кри-
сталлизации раствора с произвольным числом растворенных компонентов.
ЛИТЕРАТУРА
1.
Самарский А.А., Вабищевич П.Н
. Вычислительная теплопередача. М.: УРСС, 2003. 784 с.
2.
Samarskii A.A., Vabishchevich P.N., Iliev O.P., Churbanov A.G.
Numerical simulation of con-
vection/diffusion phase change problems — a review // Journal of Heat Mass Transfer. 1993.
Vol. 36. No. 17. P. 4095–4106.
3.
Muray W.D., Landis F.
Numerical and machine solutions of the transient heat conduction prob-
lems involving melting or freezing // Journal of Heat Transfer. 1959. Vol. 81. P. 106–112.
















