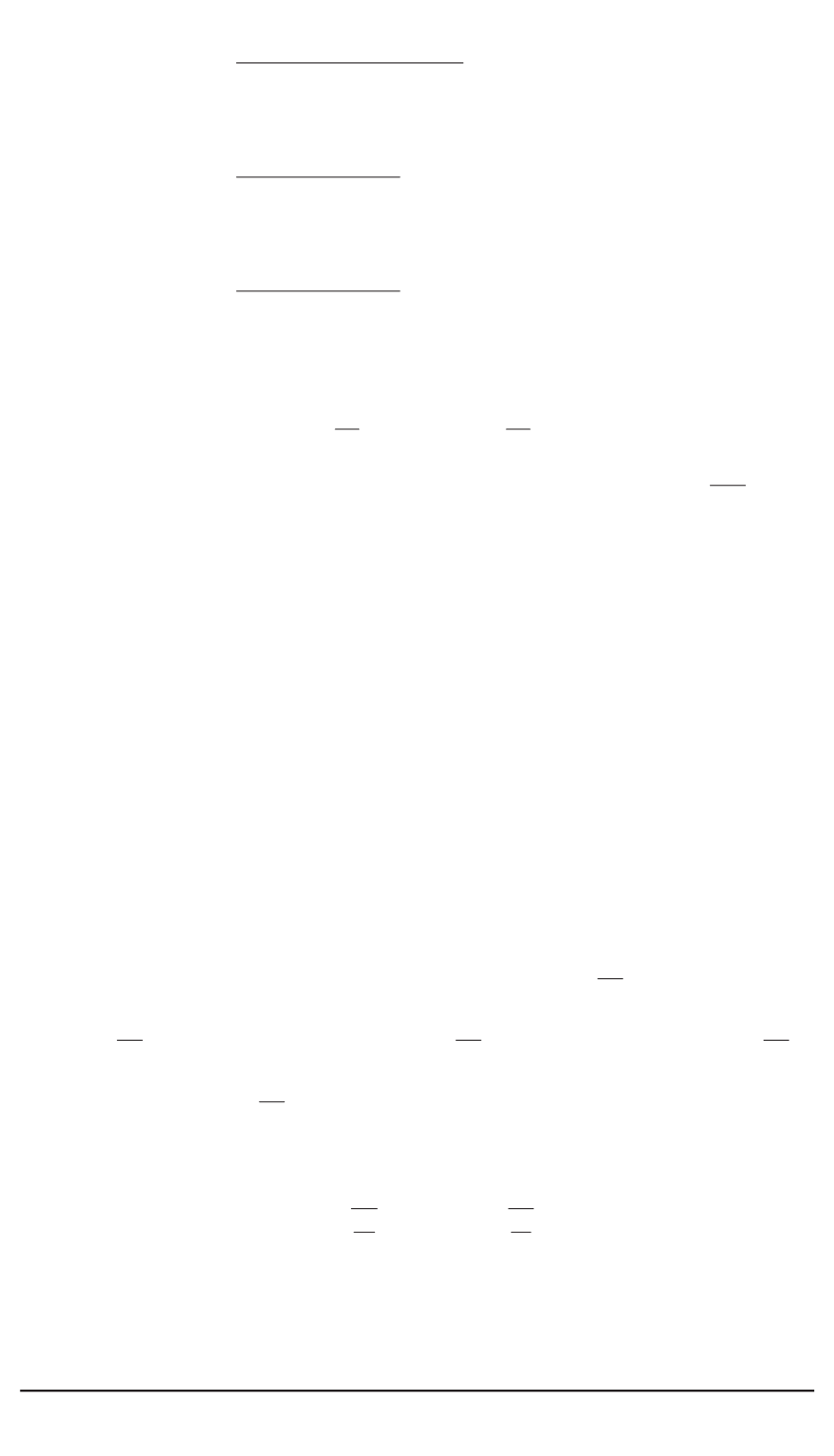
A
22
=
−
(2
n
−
1)!
ω
2
n
−
2
12
2
2
n
(
n
+ 1)!(
n
−
1)!
α
[
β
2
+ (2
n
+ 1)
ω
2
2
γ
2
−
−
δ
2
n
+2
(
β
1
+ (2
n
+ 1)
ω
2
2
γ
1
)];
A
12
=
−
(2
n
−
1)!
ω
2
n
−
2
2
2
2
n
n
!(
n
−
1)!
α
δ
2
[
−
(
β
2
+ (2
n
+ 1)
ω
2
2
γ
2
)+
+
δ
2
n
+2
(
β
1
+ (2
n
+ 1)
ω
2
2
γ
1
)];
A
21
=
−
(2
n
−
1)!
ω
2
n
−
2
1
2
2
n
n
!(
n
−
1)!
α
δ
2
[
−
(
β
1
+ (2
n
+ 1)
ω
2
1
γ
1
)+
+
δ
2
n
+2
(
β
2
+ (2
n
+ 1)
ω
2
1
γ
2
)]
.
Анализ устойчивости.
Сделаем в системе (11) замену переменных
z
1
=
√
ρ
1
e
iϕ
1
, z
2
=
√
ρ
2
e
iϕ
2
.
Тогда при
ρ
2
= 0
уравнение для
ρ
1
имеет вид
ρ
1
=
A
11
ρ
n
+1
2
1
. При
A
11
>
0
уравнение имеет неограниченно растущее решение. Из те-
оремы Четаева о неустойчивости следует неустойчивость нулевого
решения, при этом в качестве функции Четаева можно взять
V
=
ρ
1
.
Аналогично неустойчивость будет иметь место и при
A
22
>
0
.
Таким образом, при
A
11
>
0
или
A
22
>
0
равновесие исходной
системы (1)
x
1
=
x
2
= 0
,
x
1
=
x
2
= 0
будет неустойчивым.
Для асимптотической устойчивости необходимо, чтобы
A
11
<
0
,
A
22
<
0
.
Рассмотрим частные случаи. Относительно переменных
ρ
1
, ρ
2
си-
стема (11) имеет вид
ρ
1
= 2
A
11
ρ
n
+1
1
+ 2
A
12
ρ
1
ρ
n
2
;
ρ
2
= 2
A
21
ρ
2
ρ
n
1
+ 2
A
22
ρ
n
+1
2
.
(12)
Пусть
γ
1
=
γ
2
= 0
, тогда
A
11
<
0
при
δ
2
n
+2
<
β
1
β
2
, а
A
22
<
0
при
δ
2
n
+2
<
β
2
β
1
. Если
β
1
> β
2
, то
δ
2
n
+2
<
β
2
β
1
, а
A
12
<
0
при
δ
2
n
+2
>
β
2
β
1
и
A
21
>
0
при
δ
2
n
−
2
<
β
1
β
2
.
Из изложенного делаем основной вывод: равновесие асимптотиче-
ски устойчиво при выполнении неравенств
2
n
−
2
β
2
β
1
< δ <
n
+2
β
2
β
1
.
(13)
Это следует из существования положительно определенной функ-
ции Ляпунова [2]
V
=
ρ
1
+
αρ
2
, α >
0
.
(14)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 2
57