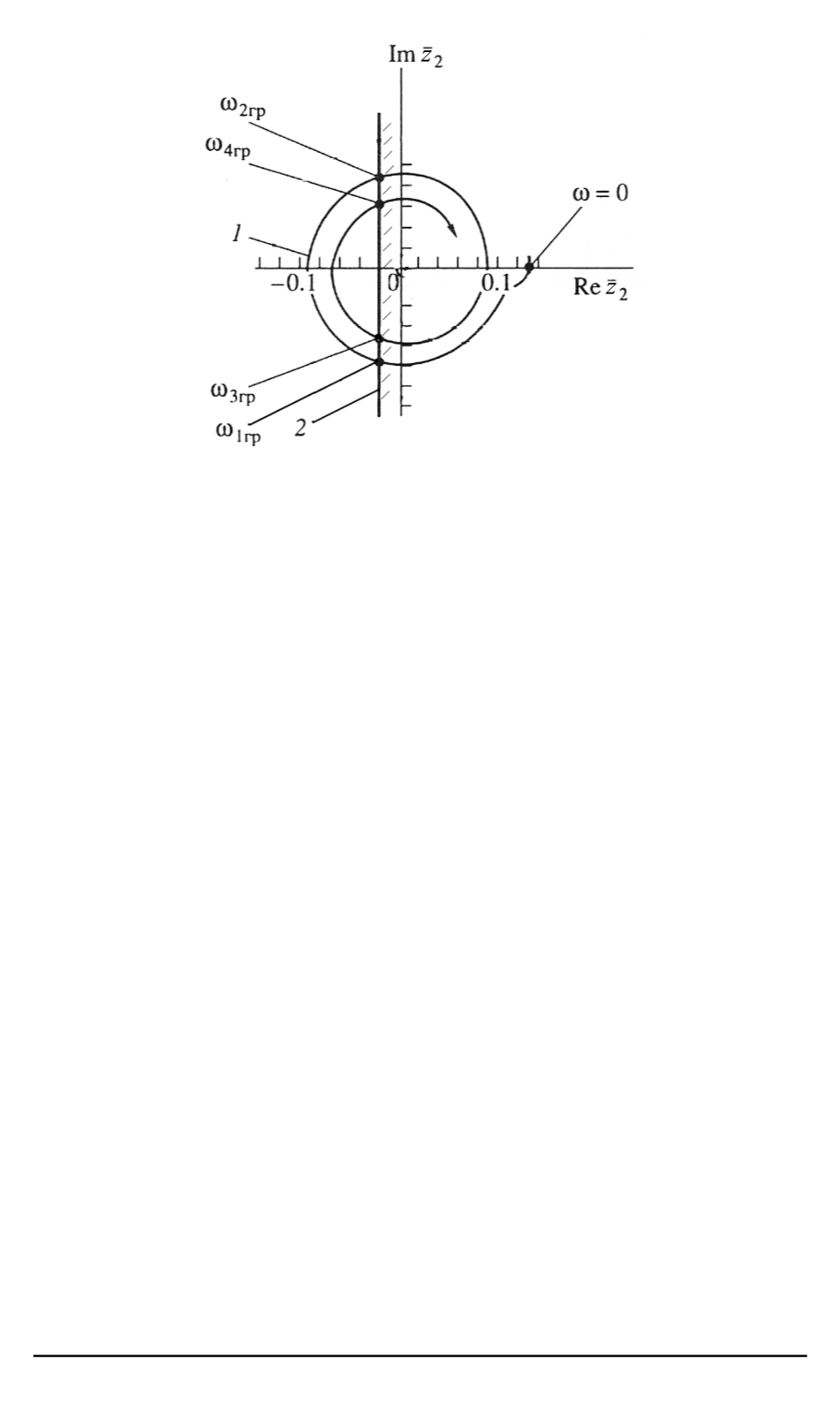
Рис. 2. Характерный вид изменения граничного импеданса в сечении 2 – 2
трубопровода на входе ограниченной искусственной газовой каверны
газовой полости;
z
00
2
=
Fρ
ж
/K
— составляющая импеданса, связанная
с учетом гидравлического сопротивления, ограничивающего участок
с расслоенным движением газа и жидкости;
B
(
ω
)
— комплекс, учиты-
вающий инерционное развитие пульсаций газовой полости.
Характерный вид зависимости
ˉ
z
2
=
z
2
(
ω
)
/z
0
(
z
0
— волновое сопро-
тивление потока жидкости в трубопроводе) на плоскости
( Re
[ˉ
z
2
(
ωτ
)]
,
Im
[ˉ
z
2
(
ωτ
)]
) иллюстрирует кривая
1
на рис. 2, имеющая
вид скручивающейся по мере увеличения фазы спирали. На том же ри-
сунке показана граница устойчивости в виде линии
2
, из пересечения
с которой находятся значения частот
ω
i
гр
на границе устойчивости, так
что частотные области неустойчивости для рассматриваемой системы
составляют диапазоны
ω
1
гр
< ω < ω
2
гр
;
ω
3
гр
< ω < ω
4
гр
.
При учете нелинейности в рассматриваемой математической мо-
дели в работах [6, 7] исследован механизм автоколебаний в системе и
показана возможность перехода к релаксационным колебаниям. При
этом учтено, что основные нелинейности, обуславливающие ограни-
чение процесса нарастания амплитуд колебаний, связаны с видом за-
висимости расхода жидкости
G
2
, поступающей на вход кавитатора, от
давления газа
p
к
в каверне
δp
к
+
ηδp
3
к
=
−
R
2
δG
2
,
(7)
где
η
— коэффициент нелинейности.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 4
121


