Эллипсоид.
Уравнение поверхности эллипсоида имеет вид
x
2
a
2
+
y
2
b
2
+
z
2
c
2
= 1
,
(5)
где
a, b, c
— полуоси эллипсоида.
Распределение поверхностной плотности электрического заряда на
уединенном проводящем эллипсоиде согласно строгому аналитическо-
му решению имеет вид [5]
σ
=
Q
4
πabc
∙
1
r
x
2
a
4
+
y
2
b
4
+
z
2
c
4
.
(6)
Обоснованием эффективности предлагаемого метода служит полу-
ченное выше соотношение
σ
(
x, y, z
)
(
~n
∙
~t
)
−
σ
(
x
0
, y
0
, z
0
)
(
~n
0
∙
~t
)
= 0
,
(7)
которое строго выполняется для поверхности (5) и распределения по-
верхностной плотности электрического заряда (6) для двух произволь-
ных точек поверхности эллипсоида.
Частные случаи рассмотренных поверхностей — эллипсоиды вра-
щения, сжатые и вытянутые эллипсоиды (сфероиды). Метод работо-
способен и для плоского случая (окружность, эллипс).
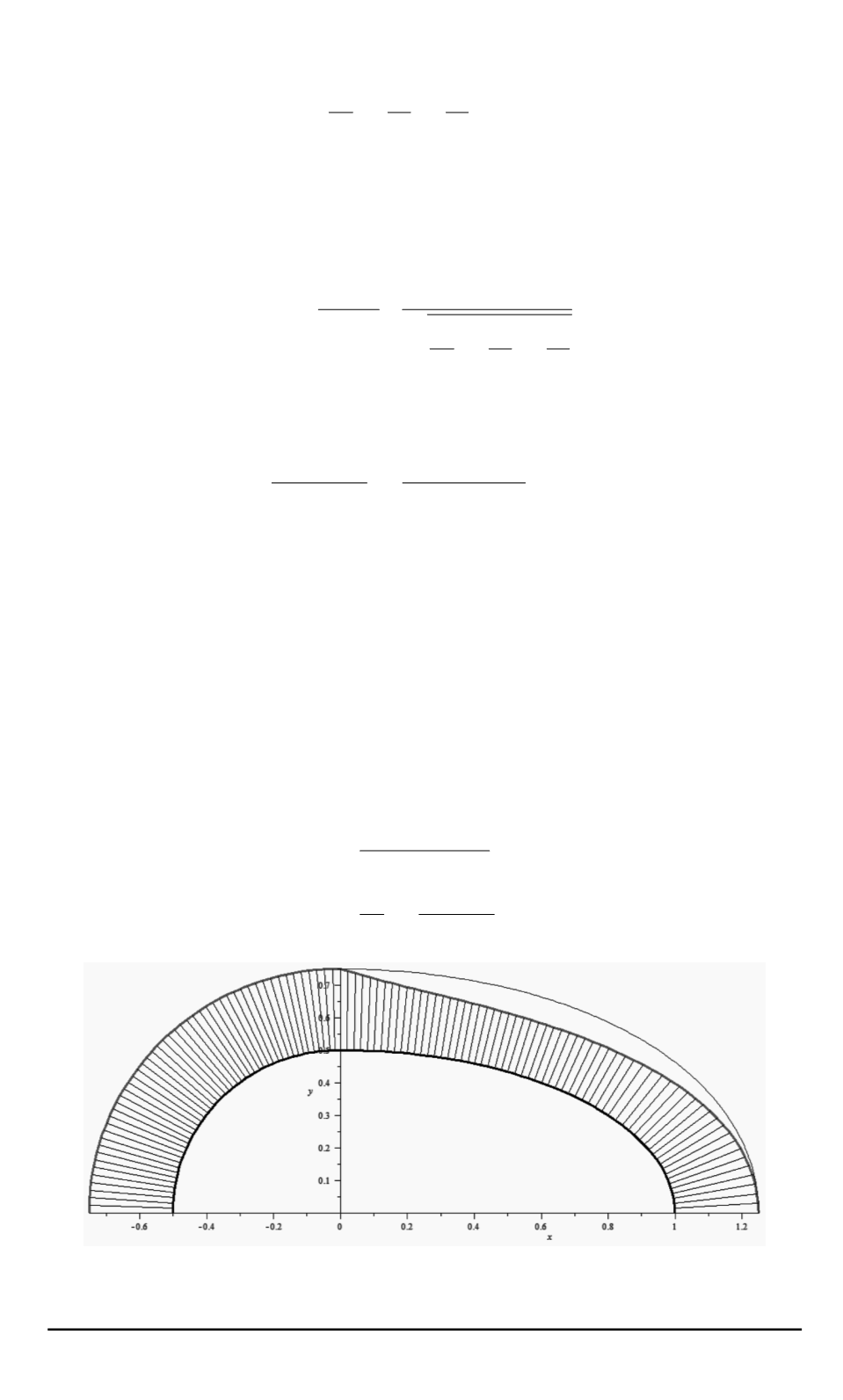
Пример сложной проводящей поверхности.
Рассмотрим пример
более сложной проводящей поверхности, описывающей гладкое со-
пряжение полусферы и полуэллипсоида (рисунок):
F
(
x, y, z
) =
x
2
+
y
2
+
z
2
a
2
= 1
, x <
0;
x
2
b
2
+
y
2
+
z
2
a
2
= 1;
x >
0
.
(8)
Распределение поверхностной плотности электрического заряда (в относитель-
ных величинах) по сложной поверхности вращения (
a
= 0
,
5
;
b
= 1
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1
23


