Применение рассмотренного метода решения задачи Робена в этом
случае более громоздко, но не представляет принципиальных затруд-
нений и доводится до конкретных числовых результатов. Однако на-
стораживает то, что поверхностная плотность электрического заряда
σ
не зависит от локальной кривизны поверхности в точках
x
=
−
a
и
x
=
b
. Для проверки правильности получаемых результатов вычислим
продольную компоненту вектора напряженности в начале координат
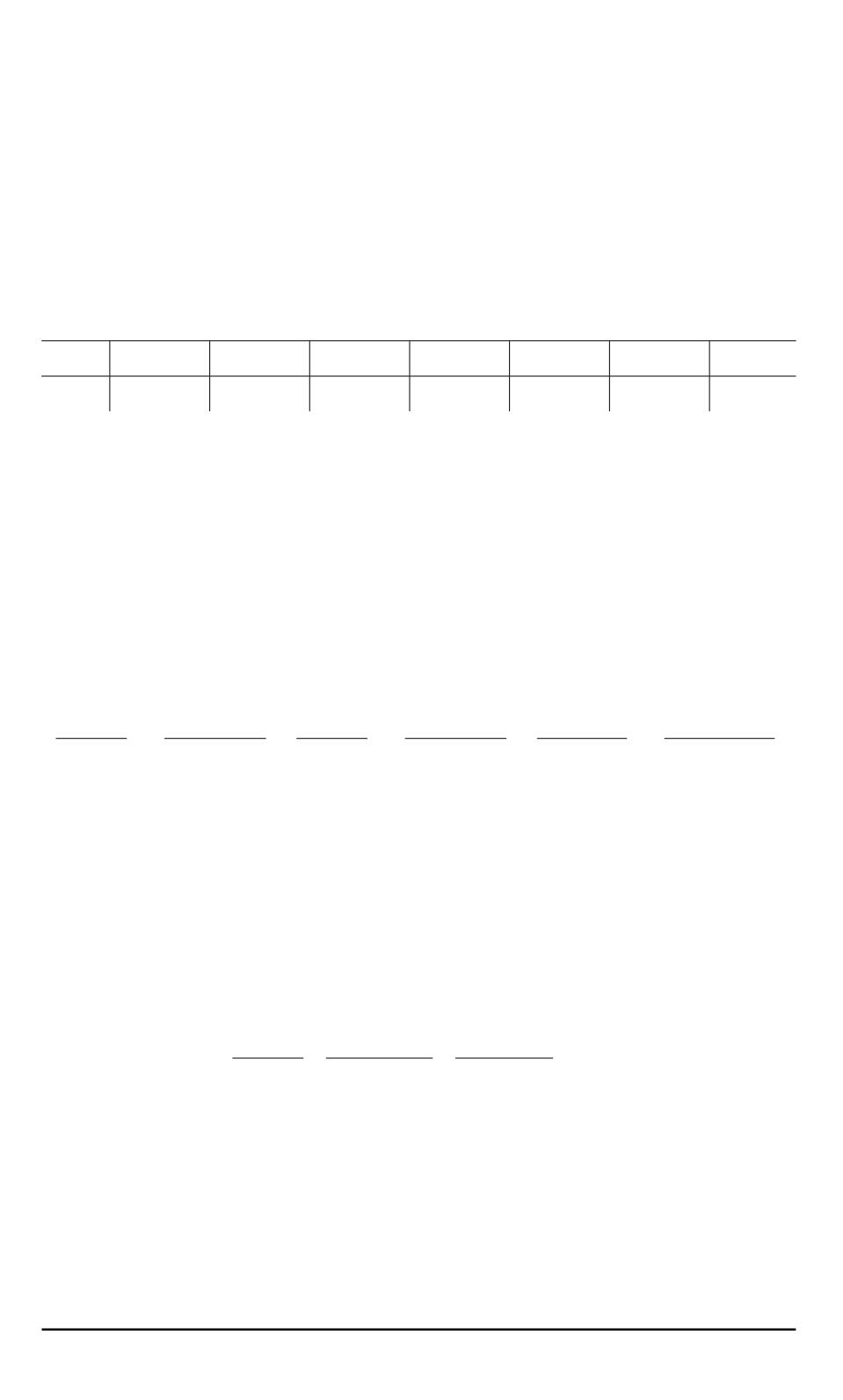
отдельно от полусферы и от полуэллипса. Результаты расчетов приве-
дены в таблице.
b
1,0
1,5
2,0
3,0
10,0
100,0
1000
E
x
3,1416 2,2475 2,0947 2,1005 2,2920 2,3653 2,3673
Из таблицы следует, что внутри рассматриваемой сложной прово-
дящей поверхности физическое условие — обращение в нуль напря-
женности электрического поля не выполнено. Интересно выяснить,
почему внешне физически правдоподобные положения приводят к не-
корректным результатам?
Рассмотрим три произвольные точки на замкнутой проводящей по-
верхности
(
x, y, z
)
,
(
x
1
, y
1
, z
1
)
и
(
x
2
, y
2
, z
2
)
. В соответствии с приняты-
ми выше предположениями должны быть справедливы соотношения
вида
σ
(
~n
∙
~t
1
)
=
σ
1
~n
1
∙
~t
1
;
σ
(
~n
∙
~t
2
)
=
σ
2
~n
2
∙
~t
2
;
σ
2
(
~n
2
∙
~t
12
)
=
σ
1
~n
1
∙
~t
12
.
Но в этом случае простой переход
(
x
1
, y
1
, z
1
) =
)
(
x, y, z
)
и сложный переход
(
x
1
, y
1
, z
1
) =
)
(
x
2
, y
2
, z
2
) =
)
(
x, y, z
)
должны приводить к одинаковому результату. Следствием этого тре-
бования является условие
(
~n
∙
~t
1
)
(
~n
∙
~t
2
)
∙
(
~n
1
∙
~t
12
)
(
~n
2
∙
~t
12
)
∙
(
~n
2
∙
~t
2
)
(
~n
1
∙
~t
1
)
= 1
.
(9)
Здесь вектор нормали к поверхности без индекса проводится в точке
(
x, y, z
)
, вектор нормали с индексом 1 или 2 — в точке, имеющей коор-
динаты с таким же подстрочным индексом, орт
~t
с индексом 1 прово-
дится вдоль направления из точки
(
x
1
, y
1
, z
1
)
в точку
(
x, y, z
)
, орт
~t
с
индексом 2 проводится вдоль направления из точки
(
x
2
, y
2
, z
2
)
в точку
(
x, y, z
)
, орт
~t
12
проводится вдоль направления из точки
(
x
1
, y
1
, z
1
)
в
точку
(
x
2
, y
2
, z
2
)
.
24
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1


