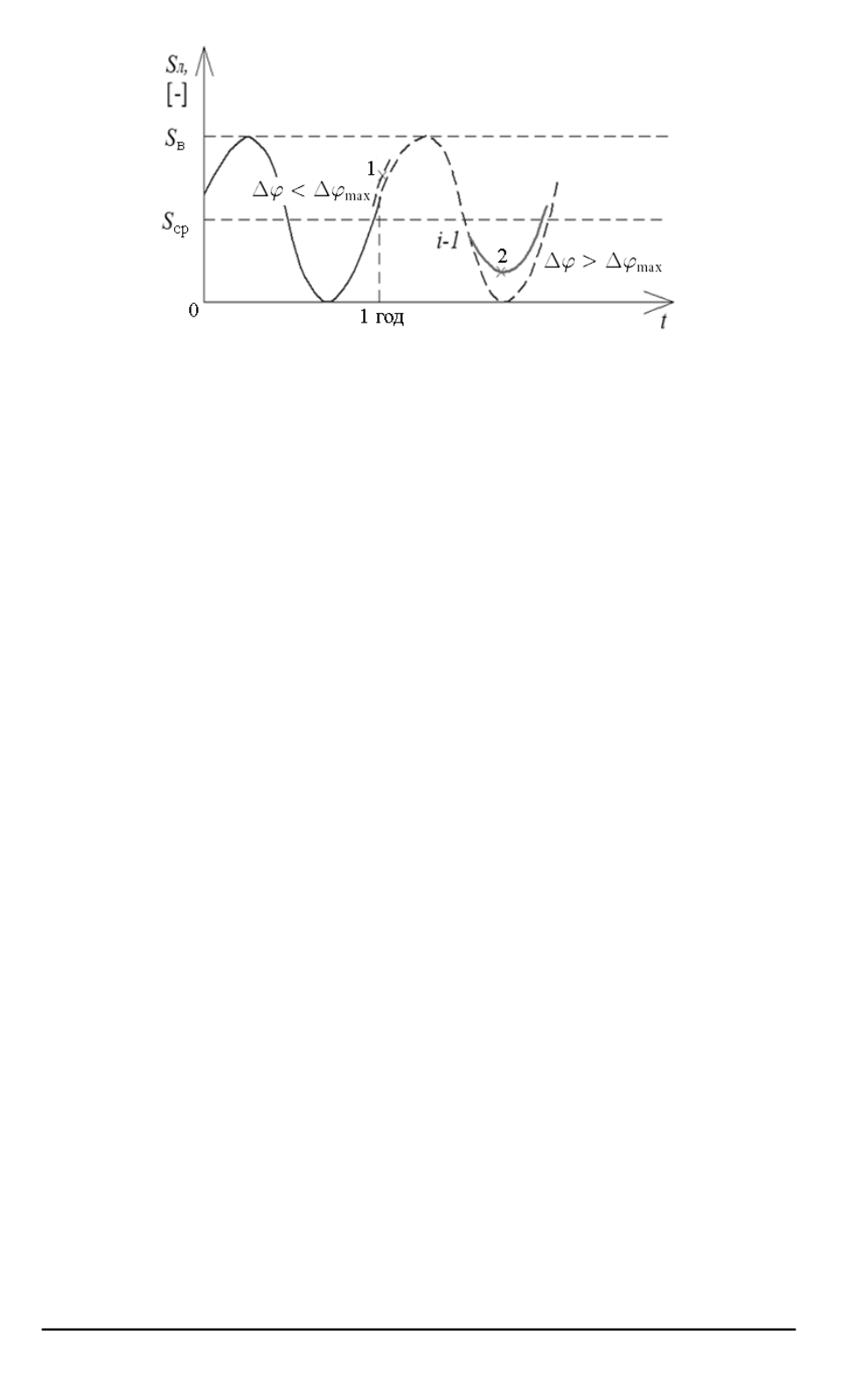
Рис. 3. Пример номинальной кривой изменения количества льда, построенной
по данным предыдущего интервала измерений (сплошная линия) и отклонений
прогнозной кривой от номинальной
Здесь необходимо учитывать, что мы ограничиваемся использова-
нием дифференциала первого порядка, что накладывает ограничения
на максимальное отклонение:
Δ
ϕ
→
0
,
Δ
ϕ <
Δ
ϕ
max
.
(4)
На рис. 3 представлена возможная ситуация, когда при прогнози-
ровании отклонение
Δ
ϕ
, вызванное изменением климатических усло-
вий, приводит к незначительному (точка 1) смещению номинальной
кривой, построенной по данным предыдущего интервала наблюде-
ний, и ситуация с резким уходом кривой от номинального положения
(точка 2). В связи с этим предлагается использовать алгоритм прогно-
зирования, в котором критерий применимости разложения в ряд
Δ
ϕ
max
определяется экспериментально.
Здесь необходимо отметить, что неизменность периода и среднего
количества льда допускается только при
ϕ < ϕ
max
, а само
Δ
ϕ
являет
собой результат воздействия всех возмущающих климатических фак-
торов в регионе. В случае если условие (4) не выполняется, на осно-
вании последних известных точек (их число определяется полнотой
модели) происходит полный пересчeт параметров синусоиды, как это
показано на рис. 4.
Для определения отклонения фазы
ϕ
от номинальной необходимо
решить обратную задачу для первой точки неноминального участка,
которая не учитывается в прогнозировании (рис. 5). Представим, что
располагая номинальной кривой, полученной по снимкам прошлого
интервала, в первой временн´ой точке прогнозируемого участка опре-
делили величину
S
л
по данным оперативной съемки. При несовпа-
дения реальной и номинальной кривых (а оно будет наблюдаться в
любом случае) в момент времени
t
i
система оказывается в том по-
ложении, которое должна по номинальной зависимости иметь в мо-
124
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1


