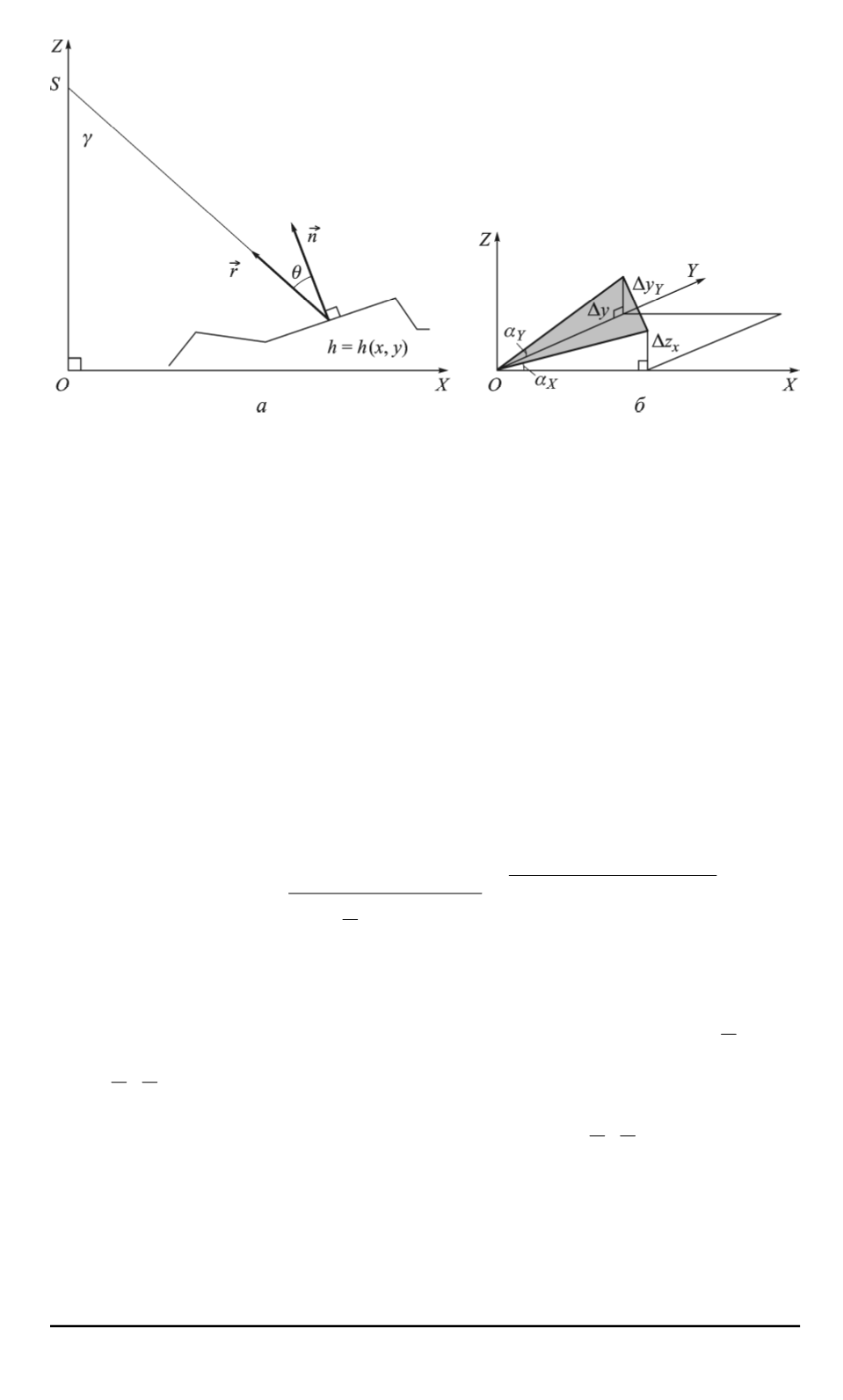
Рис. 1. К определению локального угла падения радиолокационного сигнала (
a
)
и площади фацета (
б
)
Допущение о независимости угла падения
θ
от азимутального угла
α
Y
справедливо в достаточно широкой области небольших значений
α
X
. Но в сравнительно узкой области больших значений
α
X
такая не-
зависимость уже не имеет места. Между тем интенсивность наиболее
сильно зависит от угла падения
θ
именно в узкой области больших
значений
α
X
(малых углов падения
θ
)
, поскольку вне этой области
уровень обратного рассеяния определяется главным образом другими
факторами (влажность, шероховатость). Поэтому использована более
сложная, но вместе с тем в большей степени соответствующая дей-
ствительности зависимость (1).
Площадь фацета
S
F
, выраженная через углы наклона рельефа
α
X
и
α
Y
, вычисляется по формуле
S
F
(
α
X
, α
Y
) =
Δ
a
Δ
r
cos
α
X
cos
π
2
−
γ
+
α
X
p
tg
2
α
X
+ tg
2
α
Y
+ 1
,
(3)
где
Δ
a
и
Δ
r
— размеры пикселя радиолокационного снимка по напра-
влениям азимута и наклонной дальности.
Функция
S
F
(
α
X
, α
Y
)
определена на множестве
Ω
A
=
h
γ
−
π
2
;
γ
×
× −
π
2
;
π
2
. При стремлении аргумента
α
X
слева к значению
α
X
=
γ
и аргумента
α
Y
изнутри к границам интервала
−
π
2
;
π
2
площадь эле-
мента плоскости, делающего вклад в формирование рассеянного сиг-
нала, неограниченно возрастает. Здесь проявляется ограниченность
фацетной модели. В действительности в силу причин физического
характера площадь фацета всегда остается ограниченной. В качестве
ограниченной аппроксимации функции
S
F
(
α
X
, α
Y
)
на множестве
Ω
A
102
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 4


