ние четырехосного восьмиэлектродного подвеса с электродами в виде
сферических треугольников. В приборах с полыми роторами наиболь-
шее применение нашли трехосные подвесы с сегментными электрода-
ми (подвес этого типа рассматривается в данной работе). Зададимся
рядом характерных размеров для подвеса с полым ротором:
— радиус ротора
a
= 20
мм;
— зазор при центральном положении ротора
h
= 120
мкм;
— угловой размер электрода
θ
= 35
◦
.
Для этих типоразмеров константы при коэффициентах электроста-
тической индукции (8) равны:
C
(0)
10
=
−
33
,
722
∙
10
−
12
Φ;
C
ˉ
x
10
=
−
30
,
856
∙
10
−
12
Φ;
C
ˉ
x
2
10
=
−
28
,
141
∙
10
−
12
Φ;
C
ˉ
y
2
+ˉ
z
2
10
=
−
2
,
79
∙
10
−
12
Φ;
C
(0)
00
= 372
,
93
∙
10
−
12
Φ;
C
ˉ
x
2
+ˉ
y
2
+ˉ
z
2
10
= 124
,
31
∙
10
−
12
Φ
.
Пусть
ϕ
0
э
= Δ
ϕ
max
= 800
В (такое опорное напряжение обес-
печивает троекратную перегрузочную способность подвеса) и мак-
симальное смещение, при котором еще сохраняется пропорцио-
нальное регулирование (линейная зона), составляет 10% зазора:
|
ˉ
x
max
|
=
|
ˉ
y
max
|
=
|
ˉ
z
max
|
= 0
,
1
.
Тогда, коэффициент усиления следящей
системы
k
= Δ
ϕ
max
/
|
ˉ
x
max
|
= 8000
. Максимальная оценка потенциала
при смещениях ротора в линейной зоне составляет
ϕ
0
≈
20
B и по
сравнению с уставкой потенциала является величиной незначитель-
ной.
Исследуем, как изменяется потенциал ротора при больших сме-
щениях, когда приращения потенциалов на электродах (5) выходят на
насыщение. Будем задавать смещение
d
центра ротора
O
1
из центра
подвеса
О
(
d
=
OO
1
)
в различных направлениях, которые определяют-
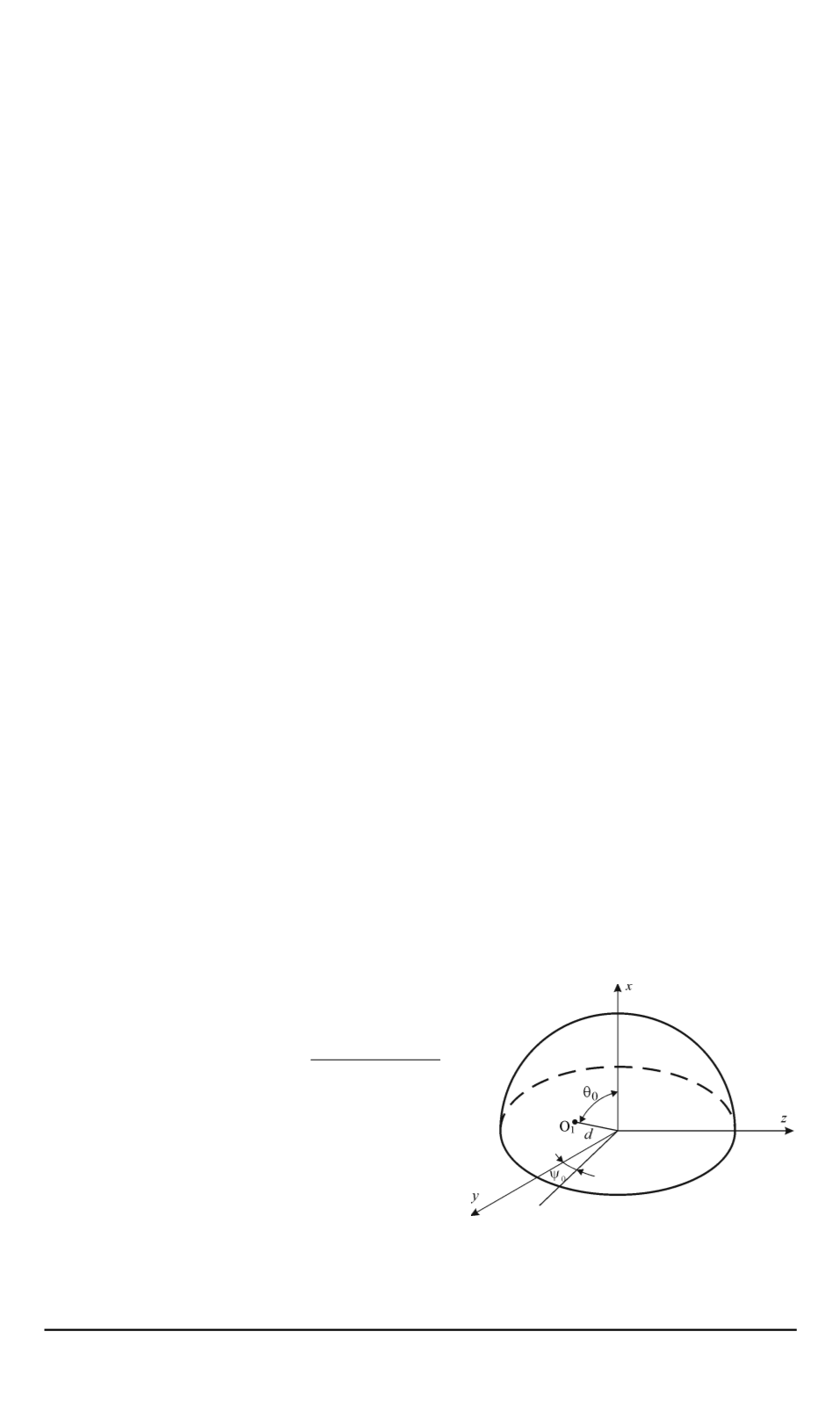
ся в сферической системе координат (рис. 2) углами
ψ
0
и
θ
0
. Линейные
Рис. 2. Система координат
смещения по осям
x
,
y
,
z
можно пред-
ставить в виде
x
=
d
cos
θ
0
, y
=
d
sin
θ
0
cos
ψ
0
,
z
=
d
sin
θ
0
sin
ψ
0
, d
=
p
x
2
+
y
2
+
z
2
.
В случае закона управления по-
тенциалами (7) (будем называть его в
дальнейшем первым вариантом упра-
вления) изменение потенциала пред-
ставлено на рис. 3. Максимального
значения
0
,
09
нормированный потен-
циал
ϕ
0
/ϕ
0
э
достигает при смещении
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1
103


