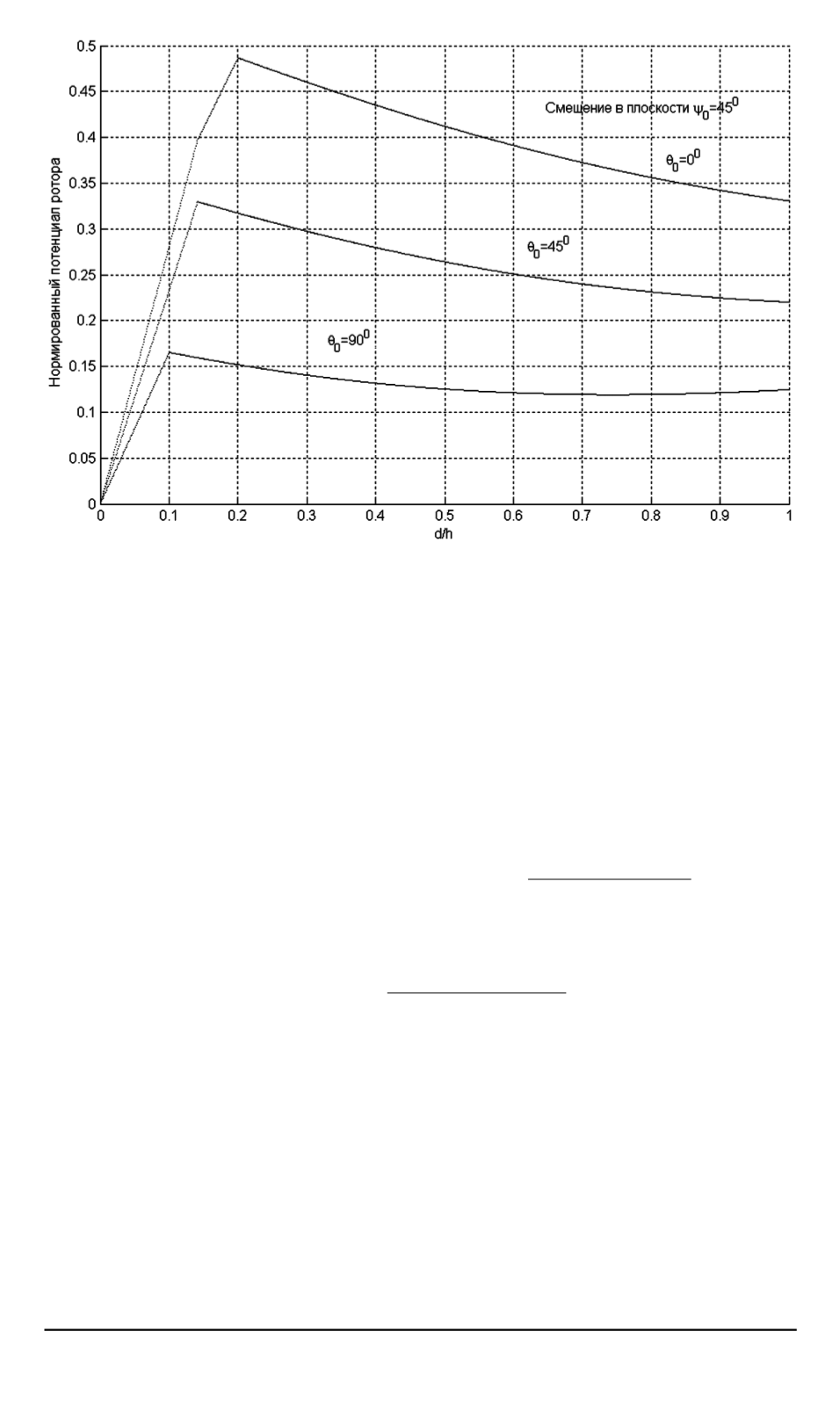
Рис. 4. Нормированный потенциал ротора подвеса с сегментными электродами
при втором законе управления
ции. Однако этот вариант обеспечивает лучшую равножесткость без
дополнительного подбора коэффициентов усиления каналов подвеса.
Чтобы сделать окончательные выводы о предпочтительности того или
иного варианта управления, рассмотрим влияние потенциала ротора
на силовые характеристики подвеса.
Найдем проекции сил
F
x
,
F
y
,
F
z
, вычисляя градиенты коэффици-
ентов электростатической индукции в (1) по соответствующим коор-
динатам
F
x
↔ r
x
C
ij
, F
y
↔ r
y
C
ij
, F
z
↔ r
z
C
ij
.
Результирующий
вектор силы по модулю будет равен
F
s
=
p
F
2
x
+
F
2
y
+
F
2
z
, а угол
ψ
между вектором силы и направлением смещения ротора можно вычи-
слить как
ψ
= arccos
F
x
x
+
F
y
y
+
F
z
z
F
s
d
.
Очевидно, что полезная составляющая силы противоположна на-
правлению смещения. Действительно, для возвращения ротора в центр
подвеса необходимо, чтобы сила и смещение имели разные знаки. На-
зовем полезную составляющую восстанавливающей силой и будем
вычислять ее как
F
=
F
s
cos
ψ
. Сила будет восстанавливающей в том
диапазоне смещений, где
F <
0
. Для обеспечения равножесткости
подвеса при работе в линейной зоне, мы вынуждены будем по оси
x
, где имеется двойная уставка напряжения, установить коэффици-
ент усиления примерно в два раза меньший, чем по осям
y
и
z
, т.е.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1
105


