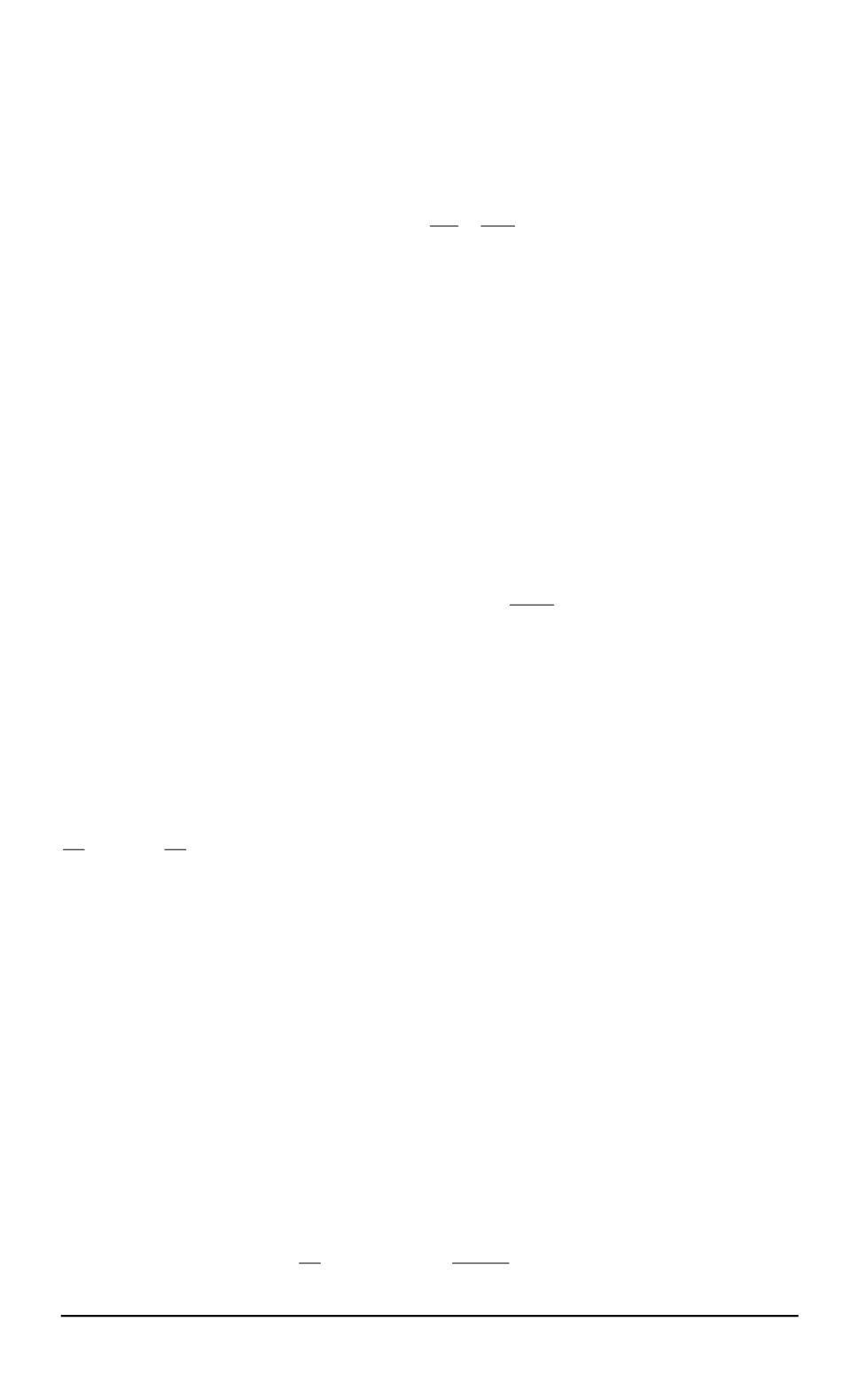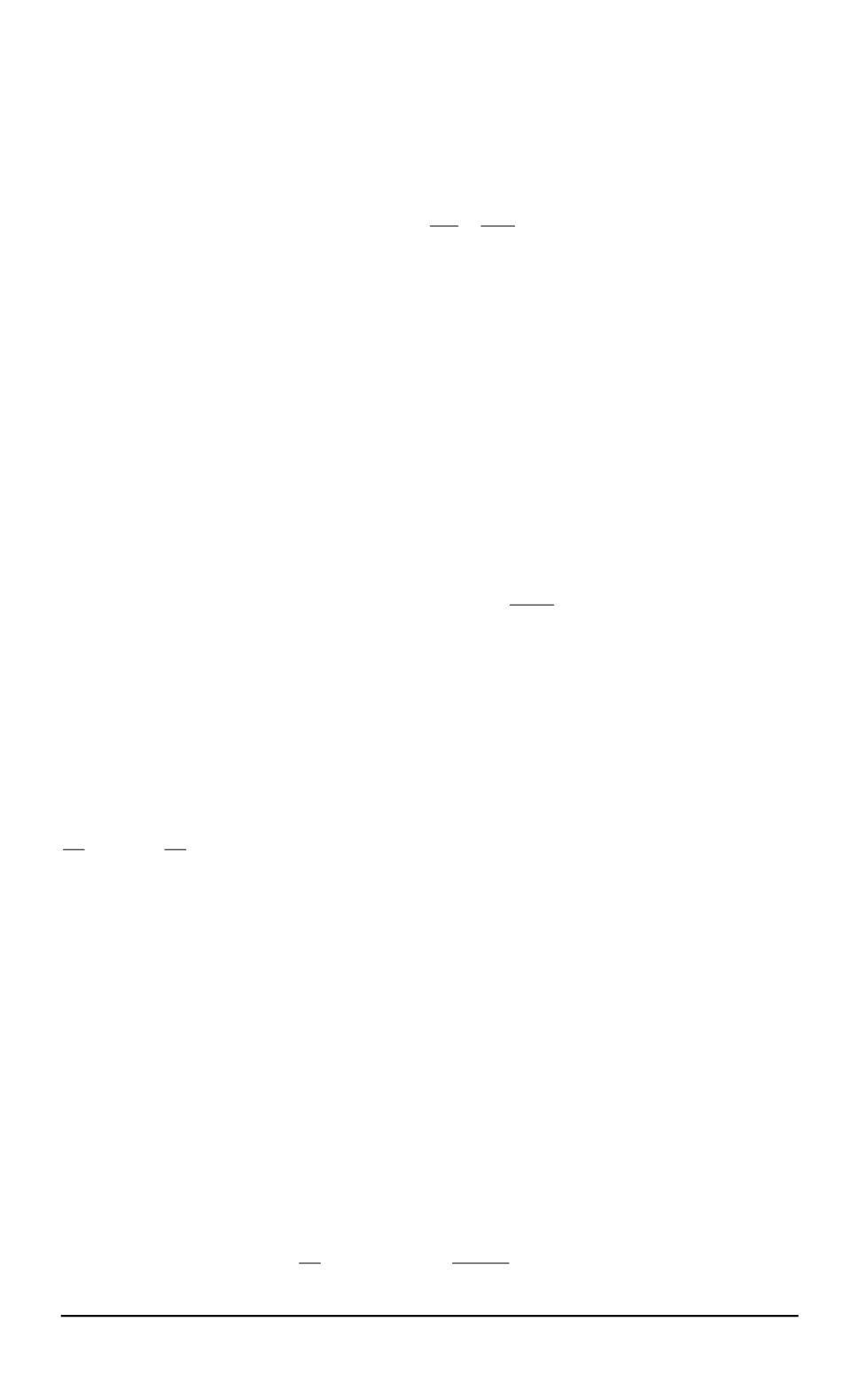
где
σ
—
сечение соударений
,
n
0
—
число частиц в единице объема
,
T
—
температура
,
m
i
—
молярная масса
,
p
—
давление
,
Ω
(1
,
1)
—
интеграл
столкновений
.
Тогда для диссипативной функции может быть предложен вид
w
=
X
i
kτ
i
R
0
n
i
dn
i
dt
2
.
(12)
Далее с учетом декларированного принципа максимальной скоро
-
сти порождения энтропии в ходе самопроизвольного химического про
-
цесса будем искать такую совокупность параметров
,
которая обеспечит
не только положительное
,
но и максимальное значение скорости возра
-
стания энтропии в соответствии с уравнением
(3).
При решении этой экстремальной задачи необходимо обеспечить
выполнение законов сохранения
,
выражающих условия существования
системы и протекания процесса
.
К ним относятся
:
а
)
условия материального баланса
(
сохранения массы химических
элементов в ходе превращений
)
X
i
a
ij
˙
n
i
= 0
, j
= 1
, m,
(13)
где
a
ij
—
стехиометрические коэффициенты
,
m
—
число химических
элементов
,
образующих систему
;
б
)
уравнение состояния идеального газа
в дифференциальной
форме
d
dt
(
pv
) =
d
dt
R
0
T
X
i
n
i
!
,
или
v
˙
p
+ ˙
vp
=
R
0
X
i
n
i
˙
T
+
R
0
T
X
i
n
i
;
(14)
в
)
уравнение
,
выражающее закон сохранения энергии
.
Внутренняя энергия многокомпонентной системы включает в себя
в том числе энергию химических связей
:
U
п
=
X
i
U
п
i
n
i
=
X
i
U
i
+ Δ
f
H
0
i
n
i
,
(15)
однако для выполнения условия постоянства внутренней энергии в
изолированной системе необходимо учитывать не только вклад квази
-
статических изменений концентраций компонентов
,
но также внутрен
-
нюю диссипацию энергии
:
d
dt
X
i
U
п
i
n
i
+
Δ
Q
вн
Δ
t
= 0
.
(16)
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
3
31