Θ
g
m
+1
/
3
0
jk
= Θ
g
m
+1
/
3
1
jk
, ρ
g
m
+1
/
3
0
jk
=
ρ
g
m
+1
/
3
1
jk
.
Условия на поверхности горения
:
~v
∙
~n
=
−
1
ρ
g
(
ρ
S
−
ρ
g
)
D,
Θ
g
= Θ
g
, ρ
g
m
+1
/
3
N
1
jk
=
ρ
g
m
+1
/
3
(
N
1
−
1)
jk
.
Граничные условия по окружной координате
:
v
gθ
m
+1
/
3
ijN
3
= 0
, v
gr
m
+1
/
3
ijN
3
=
v
gr
m
+1
/
3
ij
(
N
3
−
1)
, v
gz
m
+1
/
3
ijN
3
=
v
gz
m
+1
/
3
ij
(
N
3
−
1)
,
Θ
g
m
+1
/
3
ijN
3
= Θ
g
m
+1
/
3
ij
(
N
3
−
1)
, ρ
g
m
+1
/
3
ijN
3
=
ρ
g
m
+1
/
3
ij
(
N
3
−
1)
.
Граничные условия в выходном сечении сопла
:
(
v
gr
)
m
+1
/
3
iN
2
k
= (
v
gr
)
m
+1
/
3
i
(
N
2
−
1)
k
,
(
v
gθ
)
m
+1
/
3
iN
2
k
= (
v
gθ
)
m
+1
/
3
i
(
N
2
−
1)
k
,
(
v
gz
)
m
+1
/
3
iN
2
k
= (
v
gz
)
m
+1
/
3
i
(
N
2
−
1)
k
,
Θ
g
m
+1
/
3
iN
2
k
= Θ
g
m
+1
/
3
i
(
N
2
−
1)
k
, ρ
g
m
+1
/
3
iN
2
k
=
ρ
ge
.
Результаты численного моделирования
.
При численном решении
задачи использовались следующие данные
:
P
0
=1
∙
10
7
Па
,
D
0
=0
,
01
м
/
с
,
ν
= 0
,
4
.
Угол
θ
звездности заряда
(
см
.
рис
. 1)
был выбран равным
π
16
.
На рис
. 2–7
представлены некоторые результаты расчетов нестацио
-
нарной трехмерной задачи газовой динамики с вязким газом в различ
-
ные моменты времени
.
В табл
. 1–3
представлены значения давления
,
температуры
,
осевой и окружной составляющих скорости в различные
моменты времени
,
полученные в результате решения двумерной
(
без
учета звездности области
)
и трехмерной задач газовой динамики в слу
-
чаях идеального и вязкого газов
.
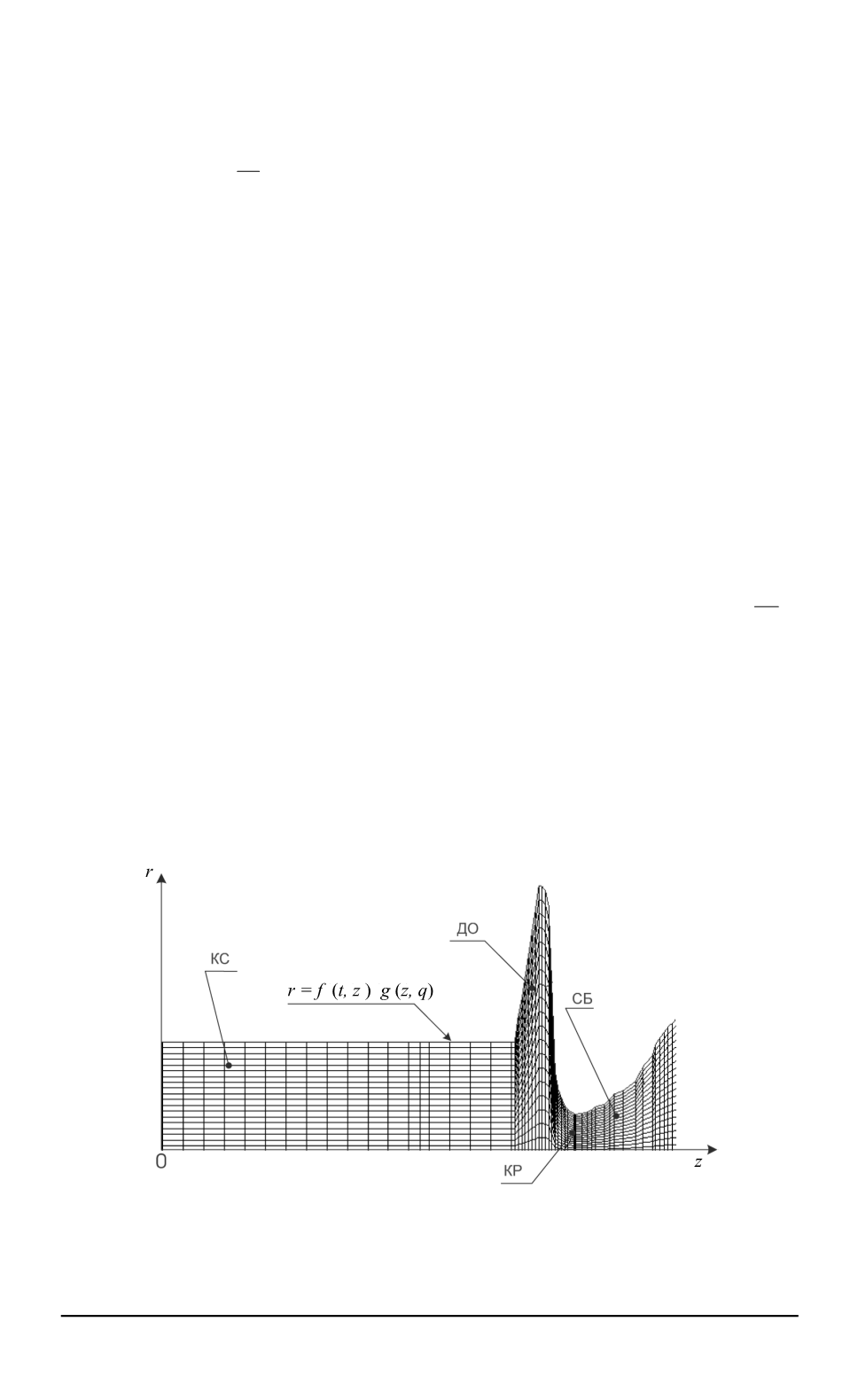
Рис
. 2.
Вид конечно
-
разностной сетки
,
использованной в задаче
:
КС
—
камера сгорания
;
ДО
—
донная область
,
КР
—
критическое сечение
;
СБ
—
сопловой блок
52
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
3


