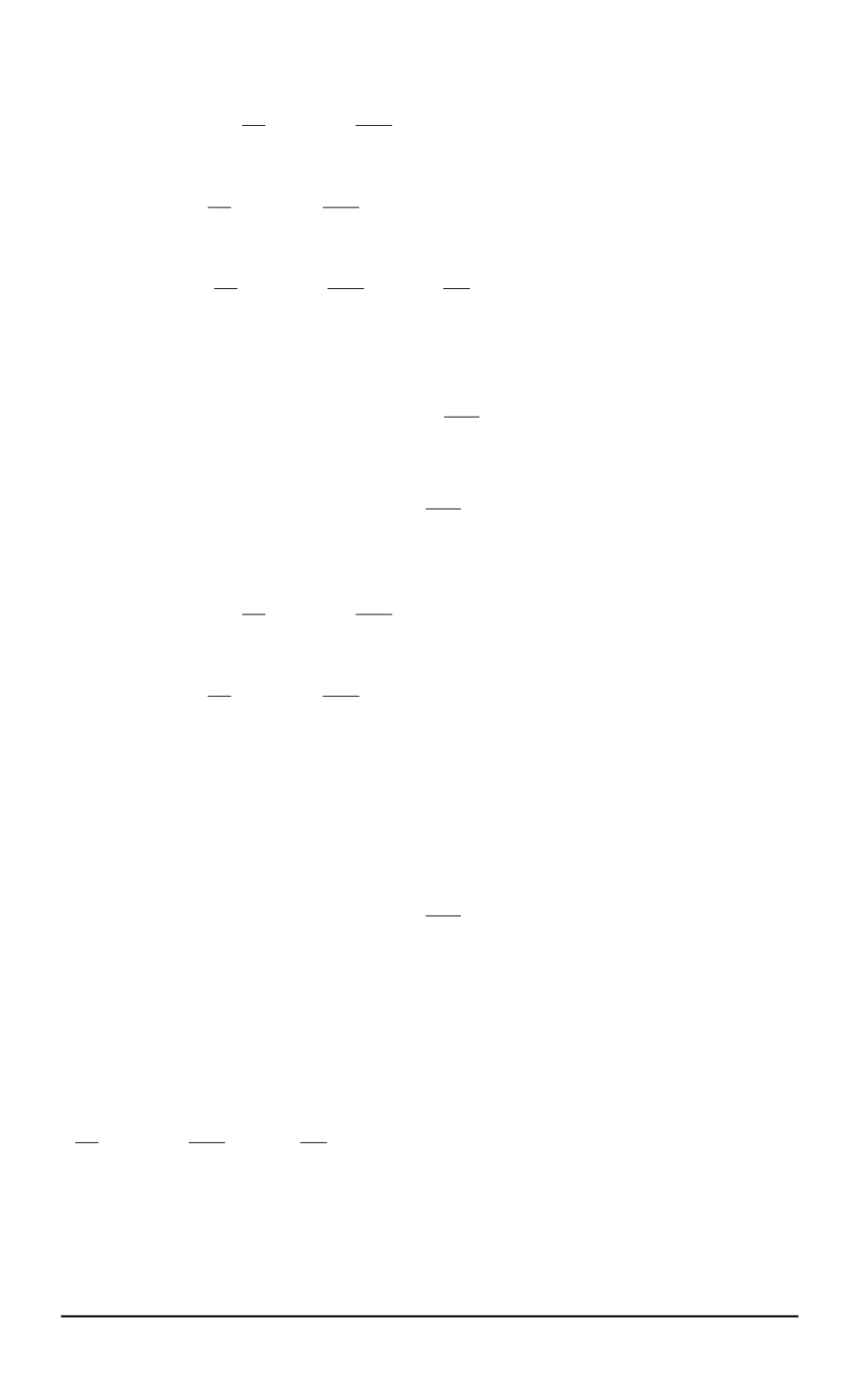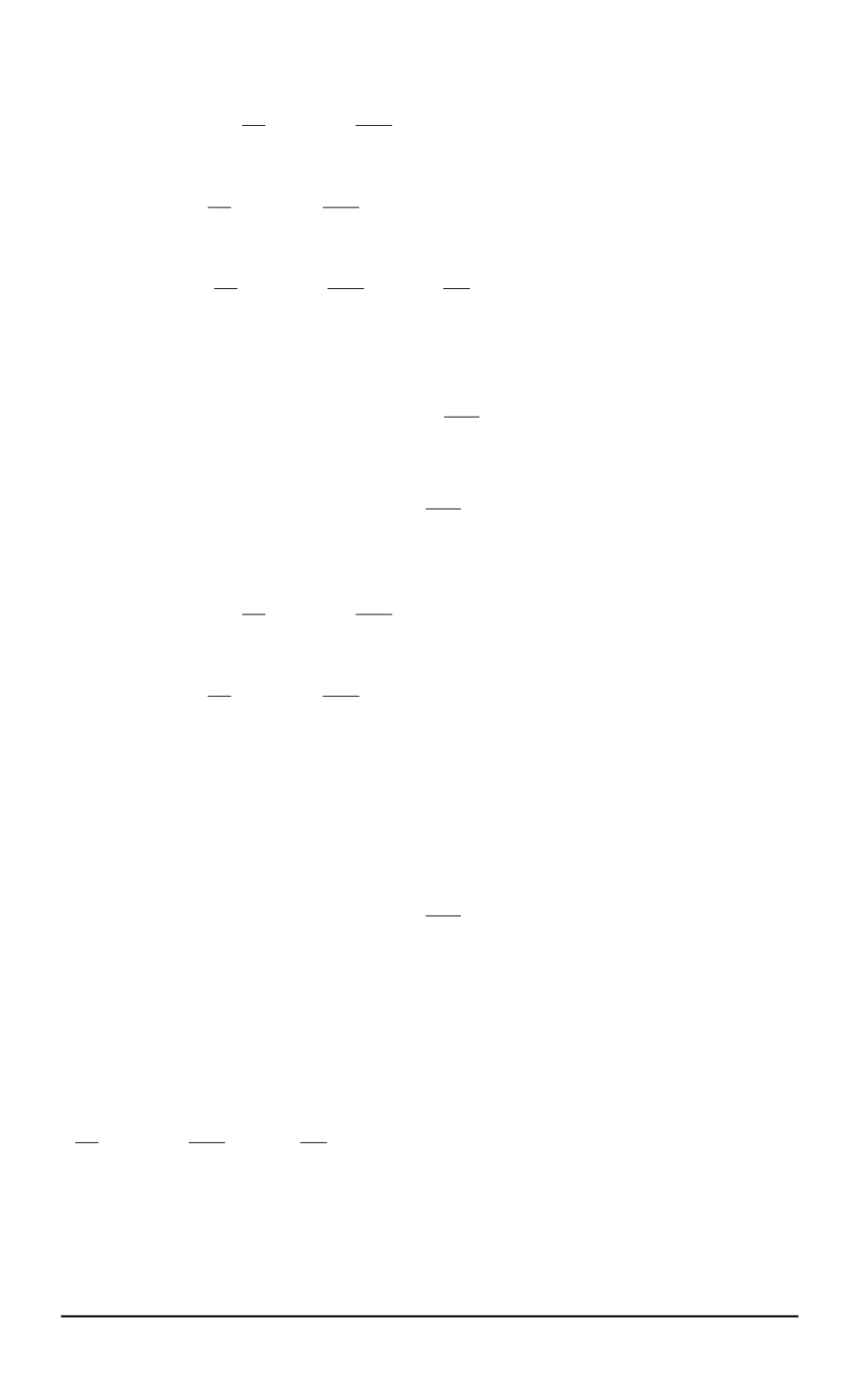
Тогда задача
(5), (6)
принимает следующий вид
:
∂
∂t
n
1
=
D
1
∂
2
∂z
2
n
1
+
a
1
,
1
n
1
+
F
1
(
z, t
)
,
∂
∂t
n
k
=
D
k
∂
2
∂z
2
n
k
+
k
X
m
=1
a
k,m
n
m
, k
= 2
,
3
,
∂
∂t
n
4
=
D
4
∂
2
∂z
2
n
4
+
v
4
∂
∂z
n
4
+
3
X
m
=1
a
4
,m
n
m
,
z
2
(0
, h
)
, t
2
(0
,
+
∞
);
(7)
n
1
(
z,
0) =
n
1
,
0
(
z
)
,
n
k
(
z,
0) = 0
, k
= 2
,
4
, z
2
(0
, h
)
,
n
k
|
z
=0
= 0
,
n
k
|
z
=
h
= 0
, k
= 1
,
4
, t
2
(0
,
+
∞
)
.
(8)
Выпишем отдельно задачу для функций
n
1
,
n
2
,
n
3
:
∂
∂t
n
1
=
D
1
∂
2
∂z
2
n
1
+
a
1
,
1
n
1
+
F
1
(
z, t
)
,
∂
∂t
n
k
=
D
k
∂
2
∂z
2
n
k
+
k
X
m
=1
a
k,m
n
m
, k
= 2
,
3
,
z
2
(0
, h
)
, t
2
(0
,
+
∞
);
(9)
n
1
(
z,
0) =
n
1
,
0
(
z
)
,
n
k
(
z,
0) = 0
, k
= 2
,
3
, z
2
(0
, h
)
,
n
k
|
z
=0
= 0
,
n
k
|
z
=
h
= 0
, k
= 1
,
3
, t
2
(0
,
+
∞
)
.
(10)
Задачу
(9), (10)
нетрудно решить
,
используя метод Фурье
(
метод
разделения переменных
).
Обозначим
˜
F
(
z, t
) =
3
X
m
=1
a
4
,m
n
m
(
z, t
)
;
тогда для определения функ
-
ции
n
4
получаем следующую задачу
:
∂
∂t
n
4
=
D
4
∂
2
∂z
2
n
4
+
v
4
∂
∂z
n
4
+ ˜
F
(
z, t
)
, z
2
(0
, h
)
, t
2
(0
,
+
∞
);
(11)
n
4
(
z,
0) = 0
, z
2
(0
, h
)
,
n
4
|
z
=0
= 0
,
n
4
|
z
=
h
= 0
, t
2
(0
,
+
∞
)
.
(12)
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
3
111