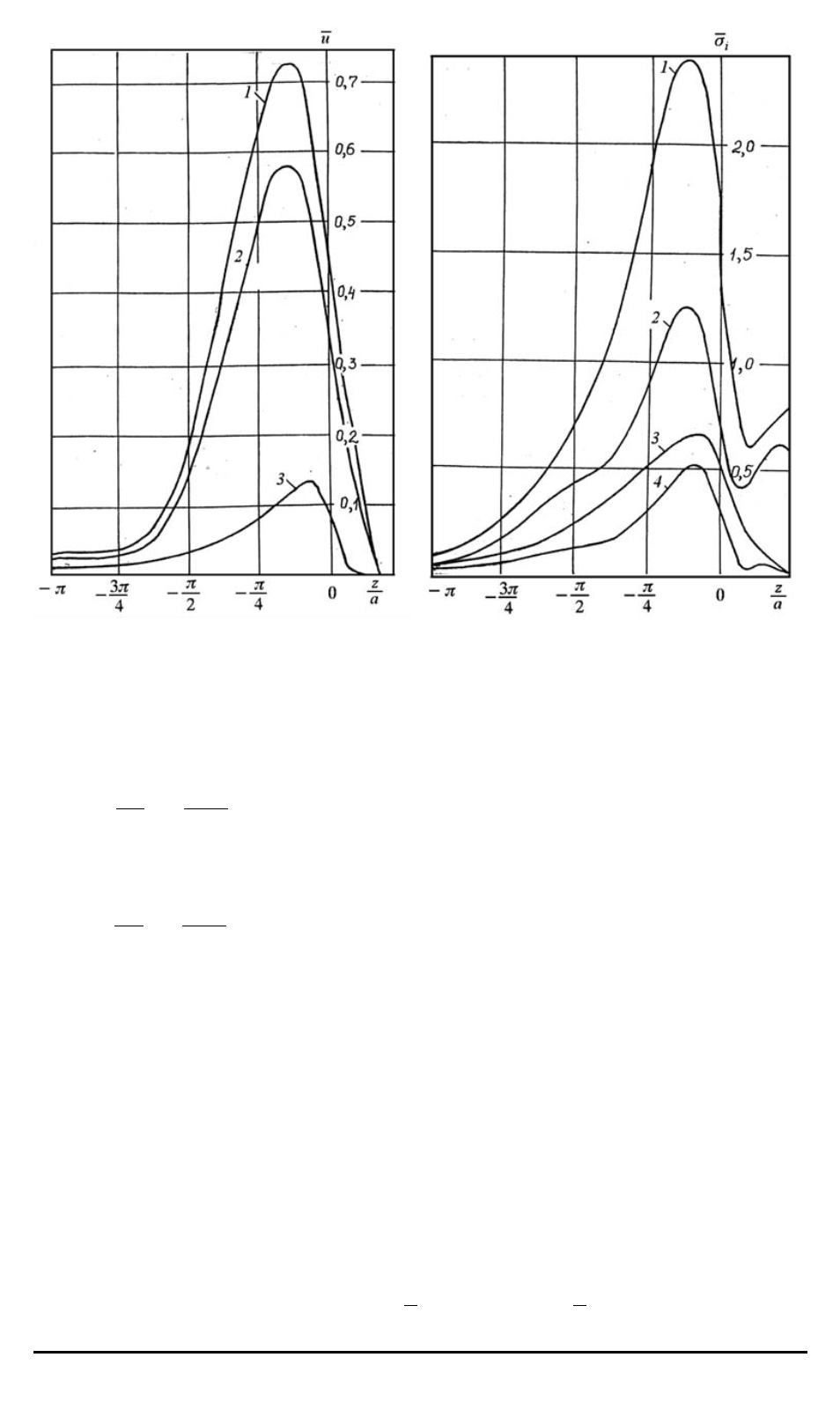
Рис. 1. Радиальные перемещения
Рис. 2. Интенсивность напряжений
Решение задачи при действии касательной нагрузки имеет вид
σ
(
q
)
r
=
1
πa
∞
0
Q
0
1
,
2
∆
η
(∆
A
2
F
1
(
r
)
−
∆
B
2
F
2
(
r
)
−
∆
C
2
F
3
(
r
) + ∆
D
2
F
4
(
r
))
dη,
τ
(
q
)
=
1
πa
∞
0
Q
1
,
2
∆
(
−
∆
A
2
f
1
(
r
) + ∆
B
2
f
2
(
r
)
−
∆
C
2
f
3
(
r
) + ∆
D
2
f
4
(
r
))
dη.
(2)
В выражениях для функций
u
(
q
)
и
θ
(
q
)
(см. формулы (1)) исполь-
зуют функции
Q
0
1
,
2
вместо
P
1
,
2
, знаки меняют на противоположные,
величины
∆
A
1
,
∆
B
1
,
∆
C
1
,
∆
D
1
— на величины
∆
A
2
,
∆
B
2
,
∆
C
2
,
∆
D
2
соответственно, которые получаютсяпри разложении определителя
∆
по элементам второй строки, и подынтегральные выраженияделят
на
η
.
В формулах (2) имеем
Q
0
1
,
2
=
Q
1
sin
η
z
a
−
Q
2
cos
η
z
a
,
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2005. № 4
55


