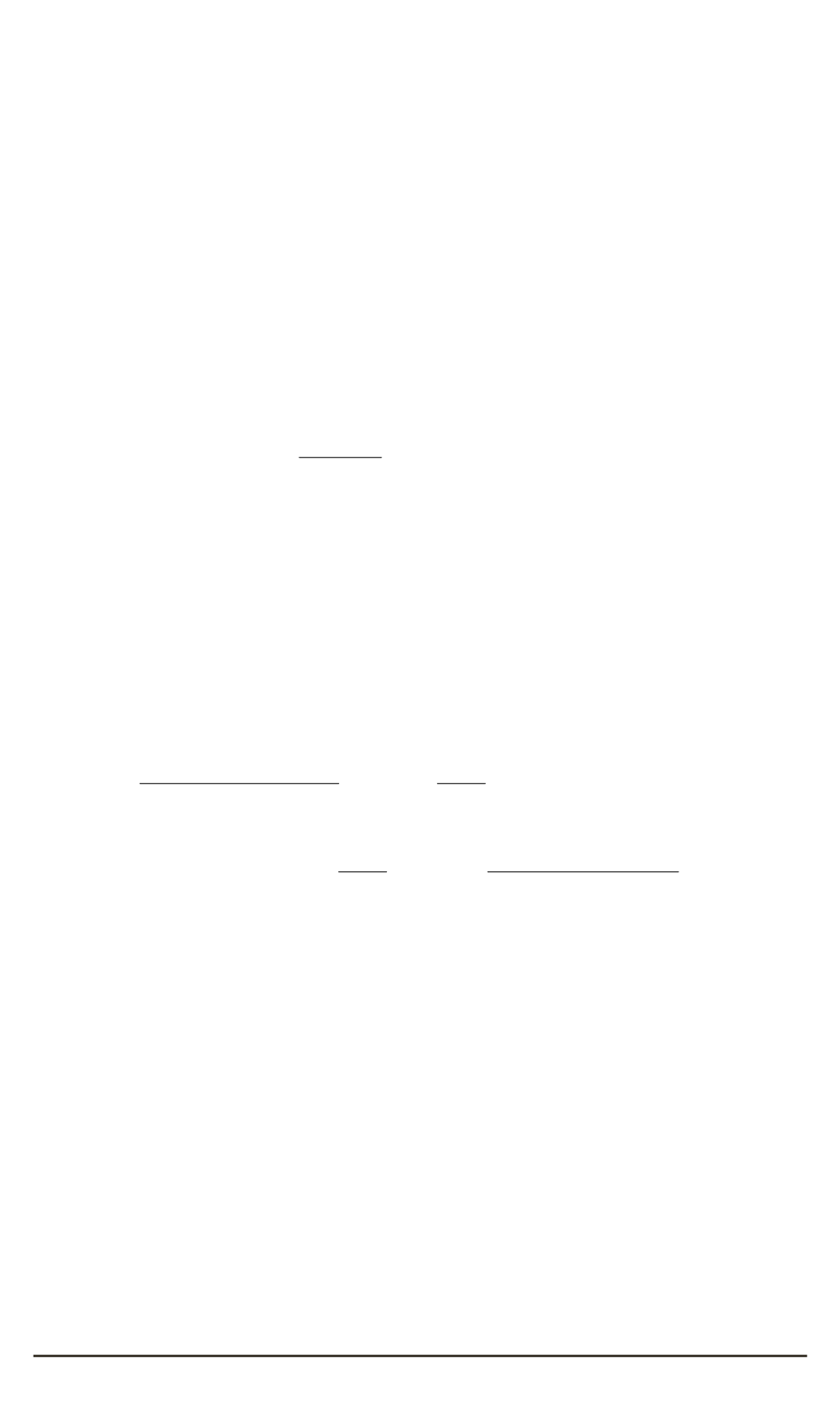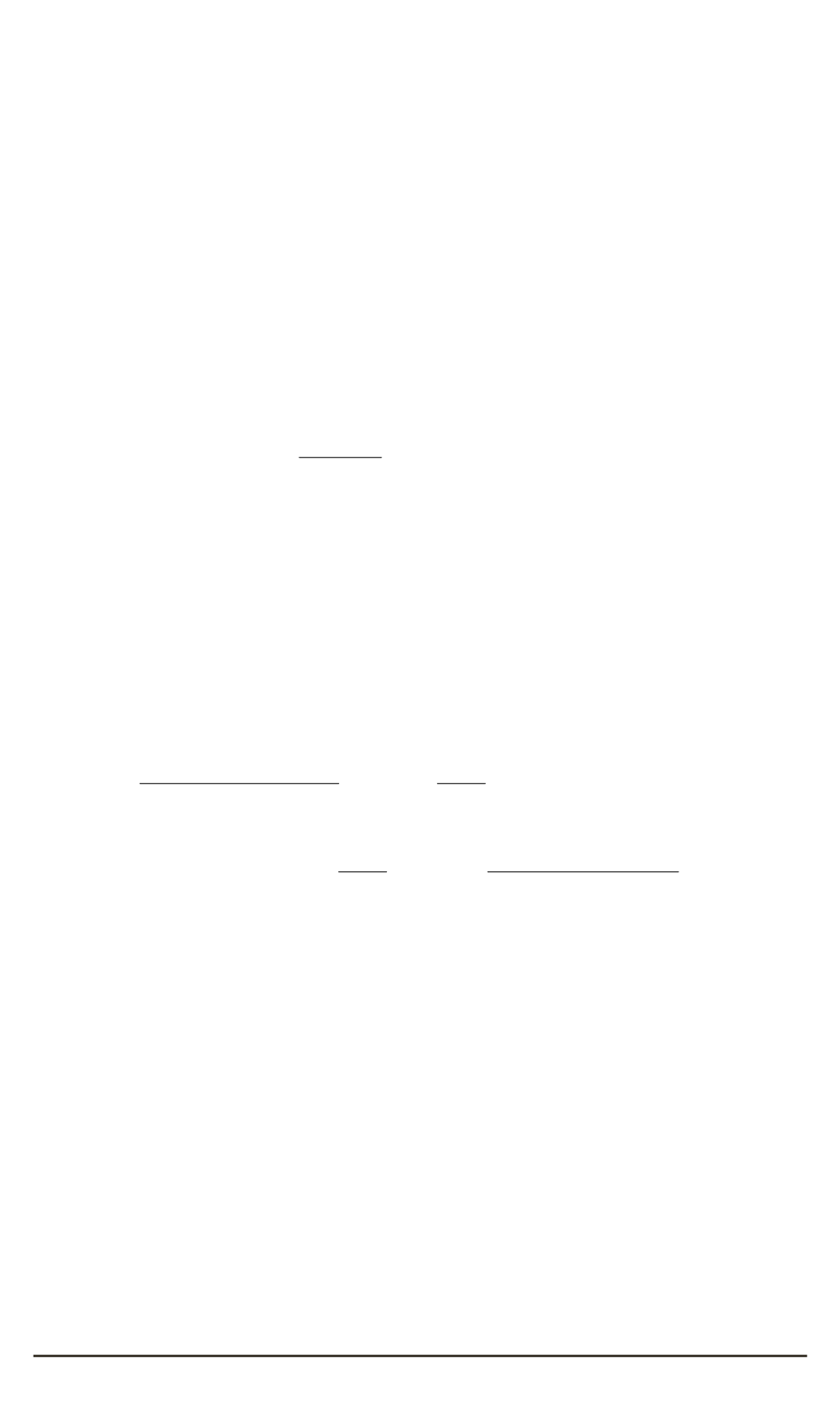
где
k
— число импульсов-спутников;
i
— порядковый номер импульса-
спутника, проходящего через среду. При выводе теоретической пере-
даточной функции образца ограничимся конечным числом импульсов-
спутников
k
, причем число импульсов-спутников
k
сигнала
E
s
(
t
)
мо-
жет быть определено программно путем его цифровой обработки.
Если волна
˜
E
0
(
ν
t
)
проходит через пустую кювету спектрометра,
комплексная амплитуда электромагнитного поля на детекторе имеет
вид
˜
E
th
r
(
ν
t
) = ˜
E
0
(
ν
t
) ˜
P
0
(
L, ν
t
)
.
(8)
Теоретический комплексный амплитудный коэффициент пропус-
кания образца может быть определен как
˜
H
th
(
ν
t
,
˜
n
0
,
˜
n
1
, l, k
) =
˜
E
th
s
(
ν
t
)
˜
E
th
r
(
ν
t
)
=
= ˜
P
0
(
−
l, ν
t
) ˜
T
01
(
ν
t
) ˜
P
1
(
ν
t
) ˜
T
10
(
ν
t
)
(
1 +
k
X
i
=1
˜
P
2
1
(
l, ν
t
) ˜
R
2
10
(
ν
t
)
i
)
.
(9)
Подставляя выражения для операторов
˜
P
0
,
˜
P
1
,
˜
T
01
,
˜
T
10
и
˜
R
10
в
выражение (9), получаем
˜
H
th
(
ν
t
,
˜
n
0
,
˜
n
1
, l, k
) =
=
4˜
n
0
(
ν
t
) ˜
n
1
(
ν
t
)
(˜
n
0
(
ν
t
) + ˜
n
1
(
ν
t
))
2
exp
−
j
2
πν
t
c
0
(˜
n
1
(
ν
t
)
−
˜
n
0
(
ν
t
))
l
×
×
1 +
k
X
i
=1
exp
−
j
2
πν
t
c
0
˜
n
1
(
ν
t
)
l
(˜
n
0
(
ν
t
)
−
˜
n
1
(
ν
t
))
2
(˜
n
0
(
ν
t
) + ˜
n
1
(
ν
t
))
2
!
i
.
(10)
Задав математическую модель теоретической комплексной пере-
даточной функции образца, перейдем к выбору метода построения
функционала ошибки
Err
, характеризующего различие теоретическо-
го
˜
H
th
(
ν
t
,
˜
n
0
,
˜
n
1
, l, k
)
и экспериментального
˜
H
exp
(
ν
t
)
коэффициентов
пропускания.
Процедура поиска оптических характеристик.
Предположим, что
известны комплексный показатель преломления воздуха
˜
n
0
(
ν
t
) = 1
,
0+
+
j
∙
0
, число импульсов-спутников
k
=
k
0
в сигнале образца и апри-
орная оценка толщины образца
l
, определенная с низкой точностью
±
(100
. . .
200)
мкм. Опишем процедуру поиска оценки оптических ха-
рактеристик образца следующим выражением:
˜
n
1
(
ν
t
) = arg min
˜
n
1
(
ν
t
)
{
Err
(
ν
t
,
˜
n
1
(
ν
t
))
}
,
(11)
78
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 3