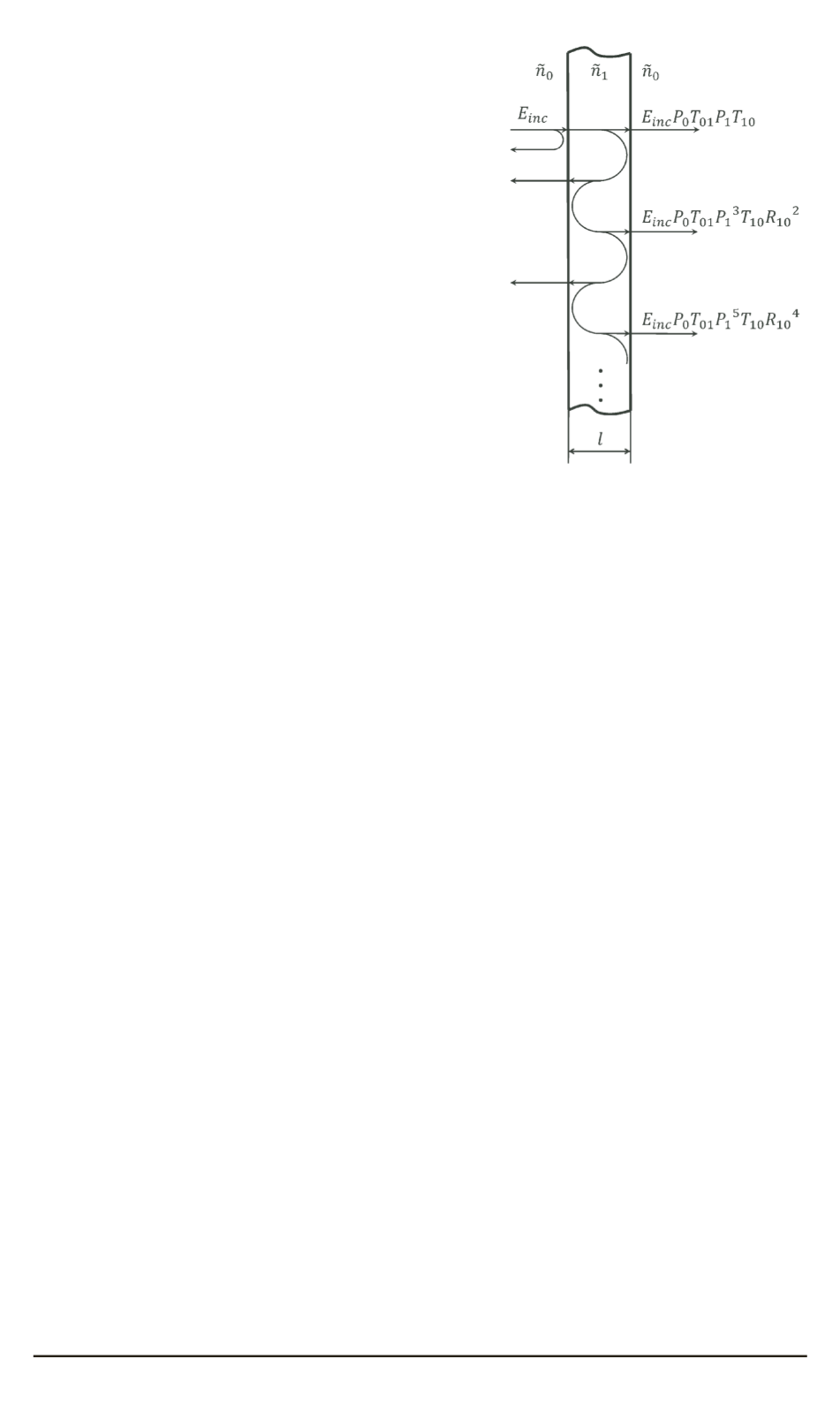
Рис. 3. Модель образца в виде
квазирезонатора Фабри – Перо
пропускания
˜
H
exp
(
ν
t
)
. Процесс поиска
комплексного спектрального показателя
преломления вещества может быть реа-
лизован в виде минимизации некоторо-
го функционала ошибки
Err
относитель-
но функции
˜
n
(
ν
t
)
. При данном подхо-
де к процессу вычисления оптических
характеристик необходимо решить две
задачи. Одна задача связана с задани-
ем физико-математической модели ТГц
спектрального коэффициента пропуска-
ния образца
˜
H
th
(
ν
t
,
˜
n, l
)
, а другая — с
определением метода построения функ-
ционала ошибки
Err
.
Модель образца.
Для вывода теоре-
тического комплексного коэффициента
пропускания плоскопараллельной плас-
тинки воспользуемся моделью квазирезонатора Фабри – Перо (рис. 3).
Полагая, что излучение падает на границы раздела сред воздух–
образец и образец–воздух нормально, используем формулы Френеля
(2) и закон Бугера – Ламберта – Бера (3) для описания прохождения
излучения через исследуемый образец.
Пусть
˜
E
0
(
ν
t
)
— комплексная амплитуда электромагнитной волны на
выходе источника импульсов ТГц-спектрометра. Обозначим
˜
n
0
(
ν
t
)
и
˜
n
1
(
ν
t
)
— комплексные показатели преломления воздуха и образца. Ком-
плексная амплитуда первого ТГц-импульса, прошедшего через образец
и достигшего ТГц-детектора, имеет вид
˜
E
0
(
ν
t
) ˜
P
0
(
L
−
l, ν
t
) ˜
T
01
(
ν
t
) ˜
P
1
(
l, ν
t
) ˜
T
10
(
ν
t
)
,
амплитуда первого импульса-спутника —
˜
E
0
(
ν
t
) ˜
P
0
(
L
−
l, ν
t
) ˜
T
01
(
ν
t
) ˜
P
3
1
(
l, ν
t
) ˜
T
10
(
ν
t
) ˜
R
2
10
(
ν
t
)
,
амплитуда второго импульса-спутника —
˜
E
0
(
ν
t
) ˜
P
0
(
L
−
l, ν
t
) ˜
T
01
(
ν
t
) ˜
P
5
1
(
l, ν
t
) ˜
T
10
(
ν
t
) ˜
R
4
10
(
ν
t
)
и т.д.
,
где
l
— толщина образца;
L
— длина оптического пути при прохожде-
нии излучения через пустую кювету ТГц-спектрометра. Суммарная
комплексная амплитуда электромагнитной волны в плоскости ТГц-
детектора составляет
˜
E
th
s
(
ν
t
) = ˜
E
0
(
ν
t
) ˜
P
0
(
L
−
l, ν
t
) ˜
T
01
(
ν
t
) ˜
P
1
(
ν
t
) ˜
T
10
(
ν
t
)
×
×
(
1 +
k
X
i
=1
˜
P
2
1
(
l, ν
t
) ˜
R
2
10
(
ν
t
)
i
)
,
(7)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 3
77


