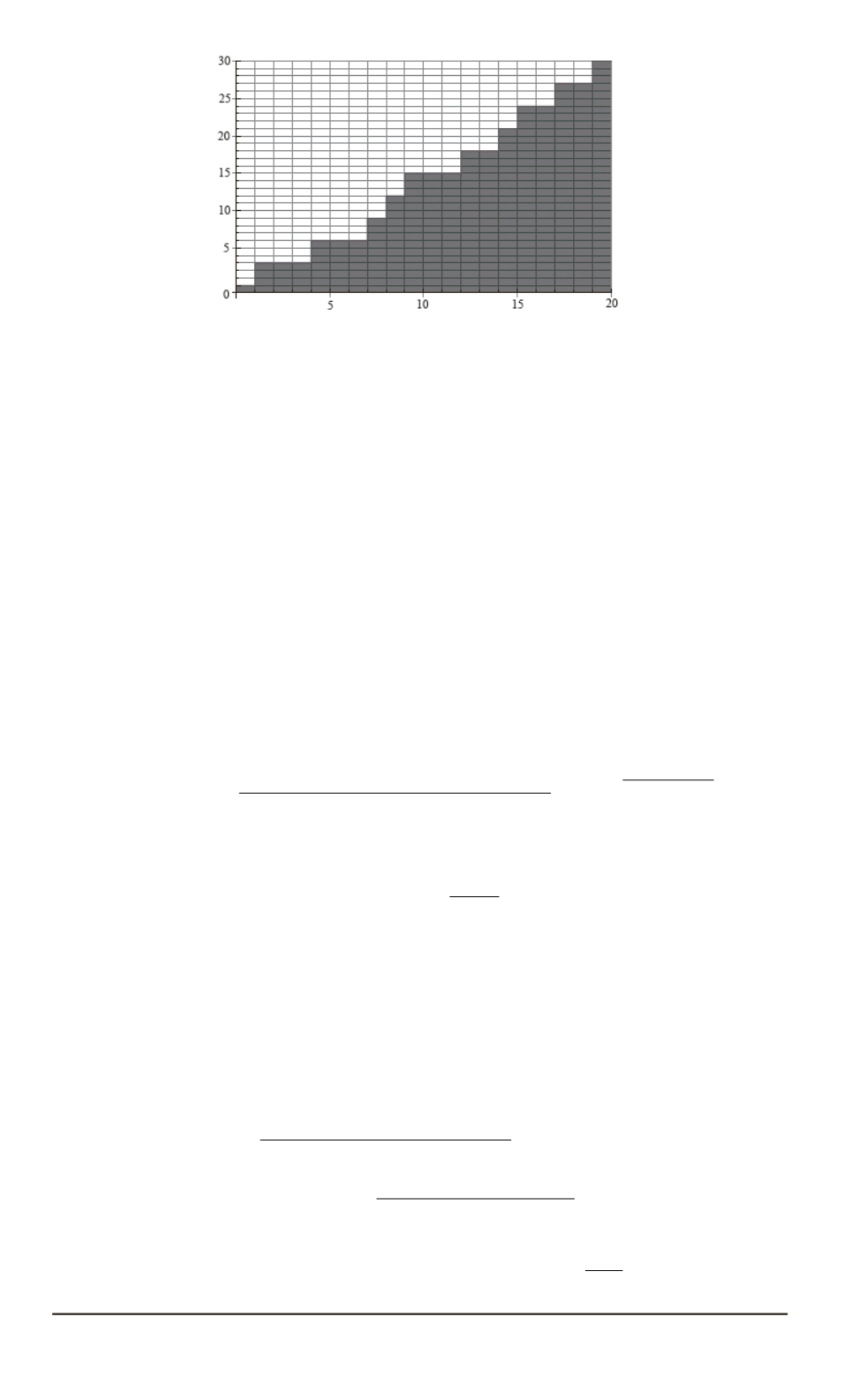
Множество ячеек случайного блуждания
то происходит скачок вправо
a
l
w
−
1
1
+
l
w
−
1
0
,l
w
−
1
2
→
a
l
w
−
1
1
+
l
w
−
1
0
+1
,l
w
−
1
2
, в про-
тивном случае вверх
a
l
w
−
1
1
+
l
w
−
1
0
,l
w
−
1
2
→
a
l
w
−
1
1
+
l
w
−
1
0
,l
w
−
1
2
+1
. Таким образом,
траектории частицы будут находиться во взаимно-однозначном соот-
ветствии с допустимыми векторами
~u
. Множество ячеек случайного
блуждания
A
~ν
при
n
= 10
,
m
= 5
показано на рисунке (
ν
1
= 2
, ν
2
= 5
,
ν
3
= 8
, ν
4
= 9
, ν
5
= 10
, ν
6
= 13
, ν
7
= 15
, ν
8
= 16
, ν
9
= 18
, ν
10
= 20
).
При фиксированном векторе
~ν
из определения оценки Капла-
на –Мейера следует, что при попадании траектории случайного блу-
ждания в ячейку
a
ij
2
A
~ν
, оценка
_
P
θ
(
t
)
принимает значения
_
P
θ
(
t
) =
p
ij
=
i
Y
d
=1
μ
d
,
μ
d
=
1
, d
= 0;
1
−
1
2
n
−
d
+ 1 + (
m
−
2) (
n
−
V
d
)
, d
= 1
,
2
n
−
1;
0
, d
= 2
n.
Аналогично
_
P
q
(
t
) =
q
ij
= 1
−
i
+
j
mn
. Тогда для статистики (5)
справедливо равенство
T
= max
i,j
ρ
(
p
ij
, q
ij
)
. Обозначим
W
i
=
i
X
k
=1
z
k
.
Теорема 1.
Вероятность
P
(
T < h/~ν
)
равна
π
2
n,n
(
m
−
2)
, которую
можно получить повторным соотношением
π
ij
=
1
,
i
= 0
, j
= 0;
π
i
−
1
,j
mn
−
V
i
(
m
−
2)
−
i
+ 1
mn
−
i
−
j
+ 1
+
+
π
i,j
−
1
W
i
(
m
−
2)
−
j
+ 1
mn
−
i
−
j
+ 1
χ
ij
, a
ij
2
A
~ν
;
0
,
(
j
=
−
1)
S
((
i
=
ν
c
−
1)
∩
((
c
−
1)(
m
−
2)+
+1
≤
j
≤
c
(
m
−
2)))
, c
= 0
, n.
12
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5


