
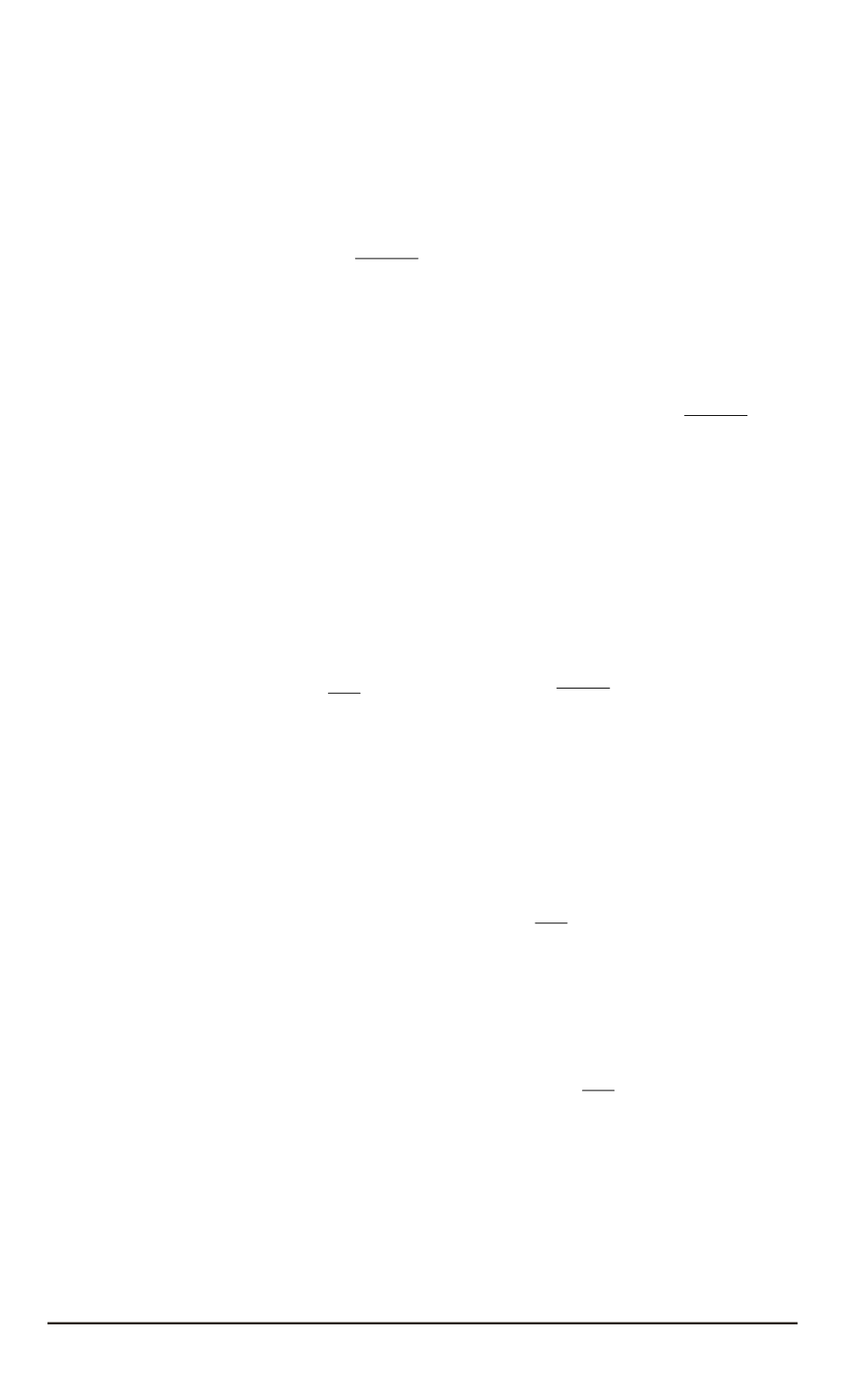
где величины
c
i
>
0
имеют смысл максимальной скорости распро-
странения сигнала в пространстве – времени с метрикой
g
(
i
)
αβ
и должны
удовлетворять следующим условиям, исключающим совпадение ме-
трик
g
αβ
,
g
(
i
)
αβ
и
g
(
j
)
αβ
:
c
(
i
)
6
= 1
, если
w
i
α
=
u
α
и
c
(
i
)
6
=
c
(
j
)
, если
w
i
α
=
w
j
α
.
Для контравариантных компонент метрики
g
(
i
)
αβ
получим
g
αβ
(
i
)
=
c
2
i
+ 1
c
2
i
w
α
i
w
β
i
−
G
αβ
,
где
w
α
i
=
G
αβ
w
i
β
. Исключая тензор
G
αβ
, находим связь между ковари-
антными и контравариантными компонентами метрик
g
αβ
и
g
(
i
)
αβ
:
g
(
i
)
αβ
=
g
αβ
−
2
u
α
u
β
+
c
2
i
+ 1
w
i
α
w
i
β
;
g
αβ
(
i
)
=
g
αβ
−
2
u
α
u
β
+
1 +
c
2
i
c
2
i
k
αβ
(
i
)
.
Здесь
k
αβ
i
= 4
u
α
u
β
u
ρ
w
i
ρ
2
−
2
u
α
w
β
(
i
)
g
+
w
α
(
i
)
g
u
β
(
u
ρ
w
ρ
) +
w
α
(
i
)
g
w
β
(
i
)
g
,
где
w
α
(
i
)
g
=
g
αβ
w
i
β
.
В случае пустого пространства метрики
g
αβ
и
g
(
i
)
αβ
должны опреде-
ляться интегралами действия
S
g
=
Z
R
g
√ −
gd
4
x
;
S
i
=
Z
R
i
p
−
g
(
i
)
d
4
x,
где
R
g
и
R
i
— тензоры Риччи метрик
g
αβ
и
g
(
i
)
αβ
;
g
и
g
(
i
)
— определители
этих метрик, причем
g
=
g
(
i
)
/c
2
(
i
)
=
−
G
[6]. Последнее равенство
позволяет объединить интегралы действия для метрик
g
αβ
и
g
(
i
)
αβ
в
один интеграл
S
Σ
=
Z (
R
g
+
n
X
i
=1
σ
i
R
i
)
√ −
gd
4
x.
Наконец, учитывая связь между метриками
g
αβ
и
g
(
i
)
αβ
и используя
хорошо известные формулы биметрического формализма, получаем
S
Σ
=
Z (
κR
g
+
n
X
i
=0
L
i
u
α
, w
(
i
)
α
)
√ −
gd
4
x,
где
κ
— некоторая константа;
L
i
u
α
, w
(
i
)
α
— функции, зависящие от
полей
u
α
,
w
i
α
и их первых производных,
w
0
α
=
u
α
.
Если учесть, что у метрик
g
αβ
и
g
(
i
)
αβ
могут быть источники, то
окончательно получим
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1
65

















