
Сравнивая соотношение (4) с дисперсионными соотношениями из те-
ории упругости для основных кристаллографических направлений,
приходим к равенствам
2
σ
1
+
σ
1
2
t
+
σ
2
2
t
=
aC
44
;
4
σ
2
=
a
(
C
12
+
C
44
) ;
σ
1
2
r
+
σ
2
2
r
−
σ
1
2
t
−
σ
2
2
t
=
a
(
C
11
−
C
44
)
.
(5)
С помощью подобранных значений силовых констант по форму-
лам (5) были вычислены значения упругих констант. При расчетах
использовалось экспериментально определенное значение параметра
решетки NiAl
2
,
887
◦
A
[1]. Результаты, полученные в настоящей работе,
и результаты расчетов, выполненных другими авторами, представлены
в таблице. Следует отметить, что в силу некоторых причин значения
упругих констант существенно расходятся со значениями, определен-
ными разными авторами, проводившими подобные исследования.
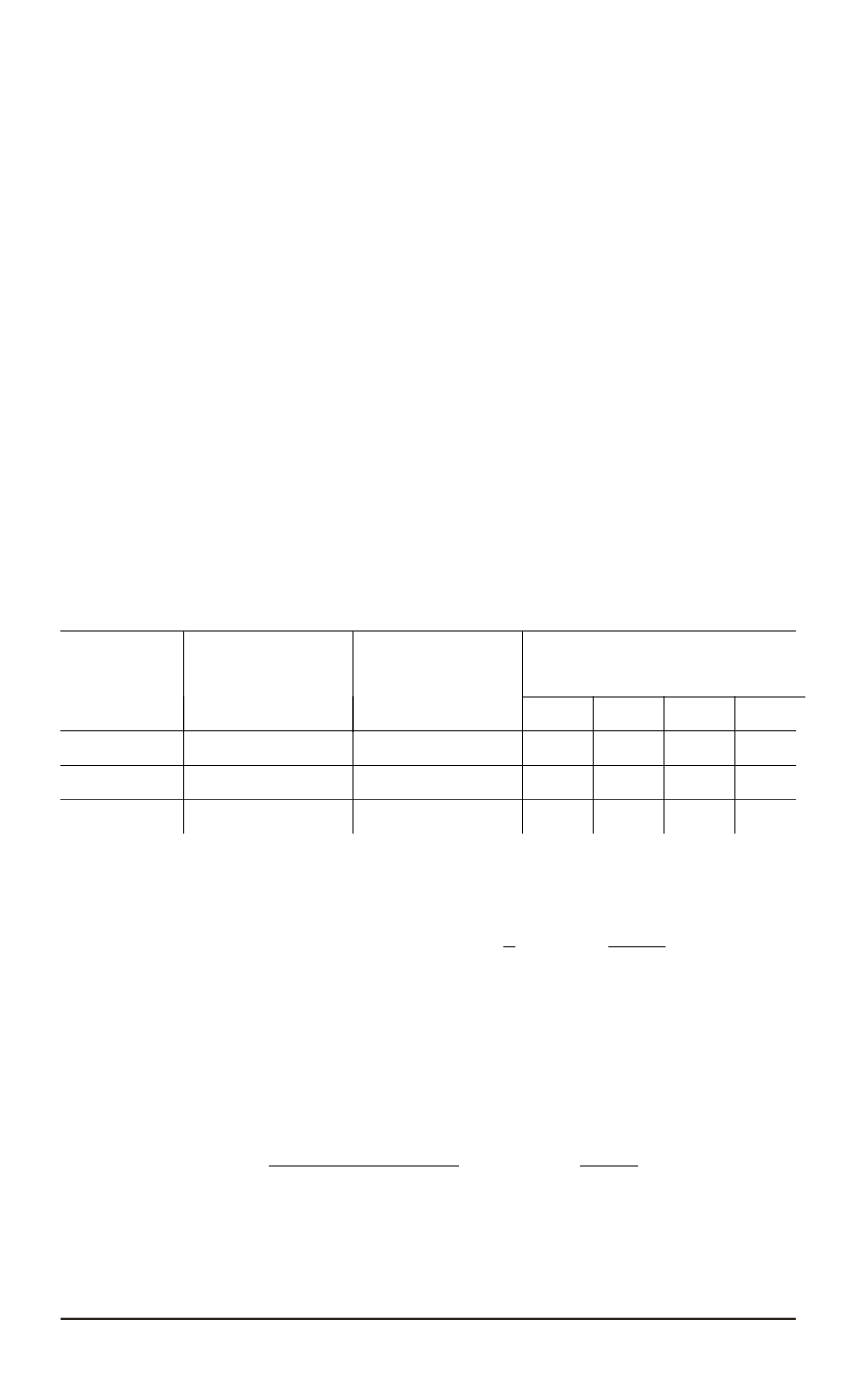
Расчетные и экспериментальные значения упругих констант NiAl
при комнатной температуре, а также значения этих констант, полученные
другими авторами
Упругая
константа
Расчетные значе-
ния, полученные
в настоящей ра-
боте
Эксперимен-
тальные значения
[12]
Значения, взятые из работ
[2]
[13]
[14]
[15]
C
11
,
(
GPa
)
177
199
197 233 159,26 202,30
C
12
,
(
GPa
)
98
137
119 121 144,14 146,10
C
44
,
(
GPa
)
83
116
110 114 93,96 100,30
Полная энергия колебательной моды частотой
ω
при температуре
T
определяется по формуле Планка
E
=
1
2
~
ω
cth
~
ω
2
k
B
T
. Согласно
классическим представлениям, вклад в эту энергию каждой подре-
шетки пропорционален произведению
μ
m
|
v
m
|
2
, и следовательно, про-
изведению
μ
m
g
m
K,j
, где
g
1
K
,j
=
x
2
1
+
y
2
1
+
z
2
1
;
g
2
K
,j
=
x
2
2
+
y
2
2
+
z
2
2
.
Таким
образом, для заданных значений
K
и
j
вклад каждой подрешетки в
полную энергию соответствующей моды описывается формулой
E
m
K
,j
=
μ
m
g
m
K
,j
2(
g
1
K
,j
μ
1
+
g
2
K
,j
μ
2
)
~
ω
K
,j
cth
~
ω
K
,j
2
k
B
T
.
Для расчета вклада каждой подрешетки в полную энергию кристал-
ла удобно использовать понятие парциальной плотности фононного
спектра
D
m
(
ω
)
:
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3
115

















