
D
m
(
ω
) =
1
6
M
Δ
ω
X
K
,m
μ
m
g
m
K
,j
μ
1
g
1
K
,j
+
μ
2
g
2
K
,j
δ
Δ
ω
(
ω
K
,m
−
ω
)
,
(6)
где
M
— число задаваемых значений вектора
K
, равномерно распреде-
ленных в зоне Бриллюэна;
Δ
ω
— условная единица длины фононного
спектра;
δ
Δ
ω
(
x
) =
(
1
,
если
x
∈
[
−
Δ
ω/
2
,
Δ
ω/
2] ;
0
,
если
x /
∈
[
−
Δ
ω/
2
,
Δ
ω/
2]
.
Формула (6) позволяет рассчитать отдельные значения парциальной
плотности фононного спектра в точках, равномерно распределенных
по всему фононному спектру с шагом
Δ
ω
.
Подобно классической формуле, выражающей температурную за-
висимость энергии кристаллической решетки, вклад каждой подре-
шетки в энергию одного моля выражается интегралом
E
m
=
3
N
A
2
ω
max
Z
0
D
m
(
ω
)
~
ω
cth
~
ω
2
kT
dω.
Аналогично, подобно классическим формулам, выражается вклад ка-
ждой подрешетки в теплоемкость кристалла, среднеквадратичные сме-
щения атомов каждой подрешетки и другие характеристики, опреде-
ляемые фононным спектром.
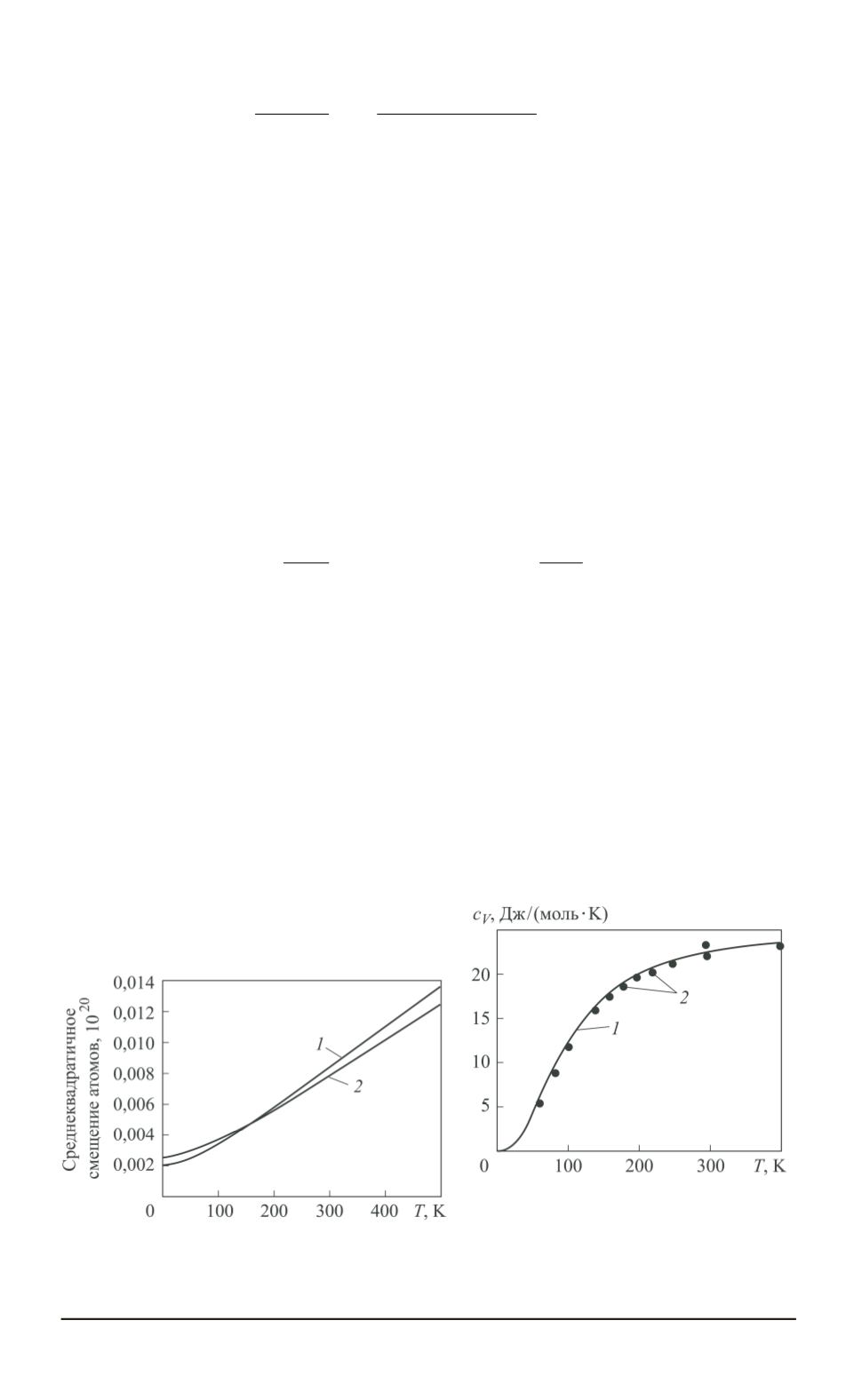
Кривые полной и парциальной плотности фононных состояний для
NiAl приведены на рис. 2, а зависимость среднеквадратичного смеще-
ния атомов от температуры — на рис. 3. В настоящей работе также бы-
ла рассчитана зависимость молярной теплоемкости
c
V
от температуры
(рис. 4). Наблюдается хорошая согласованность полученных значений
Рис. 3. Зависисмость среднеквадратично-
го смещения атомов Ni (
1
) и Al (
2
) в сплаве
NiAl от температуры
Рис. 4. Расчетная (
1
) и эксперимен-
тальная (
2
) зависимость моляр-
ной теплоемкости NiAl от темпе-
ратуры (экспериментальные дан-
ные взяты из работы [16])
116
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3

















