
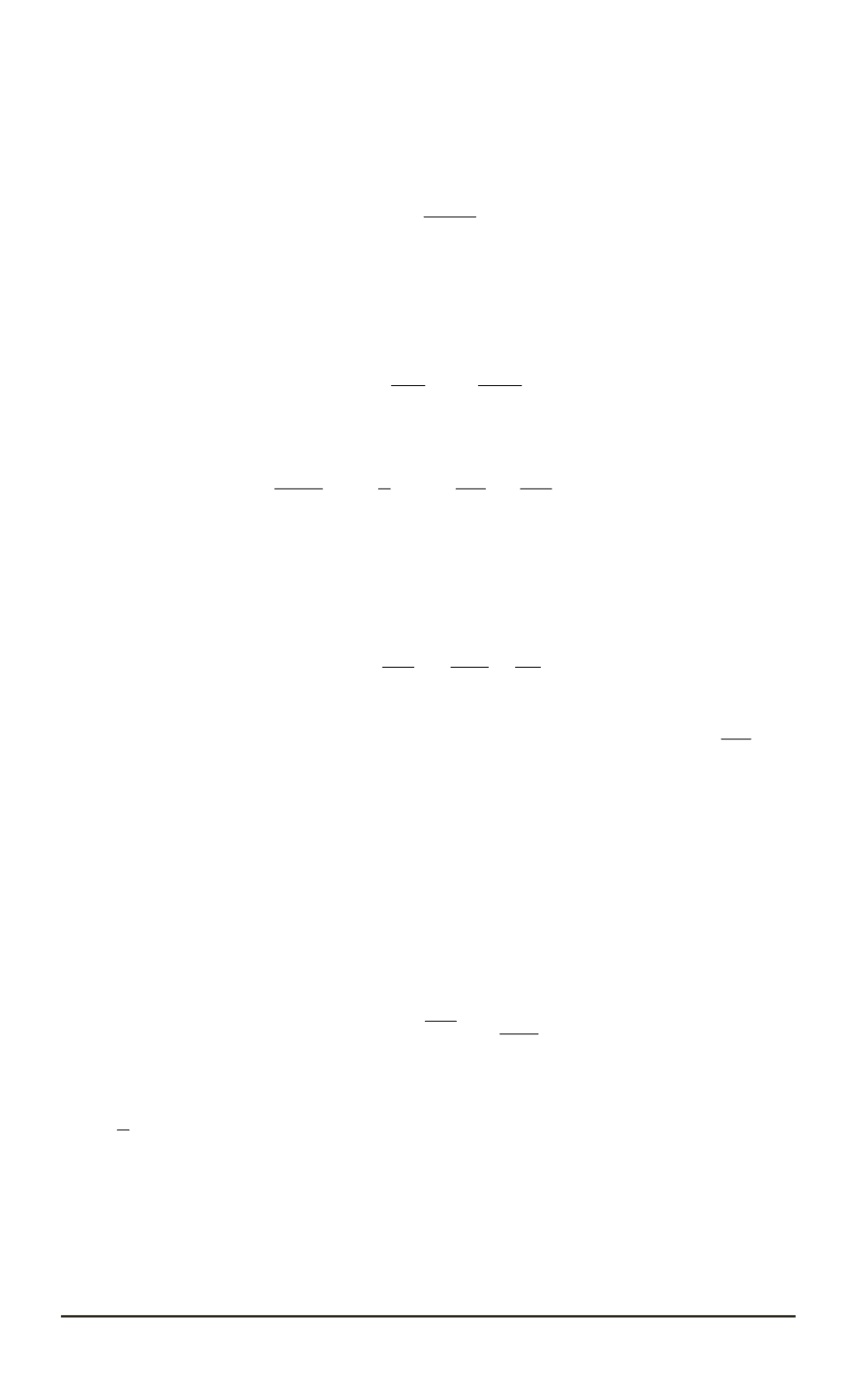
1. Потенциальная энергия поля больше кинетической
V
(
φ
) ˙
φ
2
.
2. Ограничение на вторую производную скалярного поля
¨
φ
3
H
˙
φ
.
В таком случае космологические уравнения динамики поля и рас-
ширения Вселенной будут иметь вид
H
2
'
V
(
φ
)
3
M
P
;
(4)
3
H
˙
φ
' −
V
0
φ
(
φ
)
.
(5)
Oпределим параметры медленного скатывания.
Разделим уравнение (5) на
3
H
и возьмем производную по времени.
В результате получим
¨
φ
=
−
V
00
3
H
˙
φ
+
V
0
3
H
2
˙
H
. После деления обеих
частей на
3
H
˙
φ
имеем
¨
φ
3
H
˙
φ
=
−
1
3
M
2
P
V
00
V
−
˙
H
H
2
!
.
Следует отметить, что было использовано приближенное уравне-
ние (4).
Теперь можно записать параметры медленного скатывания
ε
(
φ
)
∼
=
−
˙
H
H
2
=
M
2
P
2
V
0
φ
V
,
где
V
0
φ
— производная потенциала
V
(
φ
)
по полю
φ
,
η
(
φ
) =
M
2
P
V
00
V
.
Параметр
ε
показывает, насколько параметр
H
изменился со вре-
мени инфляции. Таким образом,
¨
a/a
= ˙
H
+
H
2
= (1
−
ε
)
H
2
,
инфляция
может быть достигнута только при
ε <
1
. В общем случае режим
медленного скатывания может быть достигнут, если
ε
1
и
η
1
.
Однако эти условия только ограничивают форму потенциала [5].
Модели с нетривиальной кинетической частью.
Запишем дей-
ствие, описывающее скалярное поле, которое взаимодействуeт с гра-
витационным следующим образом [7]:
S
=
S
g
+
S
φ
=
Z
d
4
x
√ −
g
−
R
16
π
+
p
(
φ, X
)
,
где
R
— скаляр Риччи;
p
(
φ, X
)
— функция скалярного поля
φ
;
X
=
1
2
∇
μ
φ
∇
μ
φ
.
В случае обычного скалярного поля зависимость величины
X
от
величины
p
тривиальна:
p
=
X
+
V
(
φ
)
, в то время как
k
-инфляция
основана на нетривиальной зависимости
p
от
X
. В случае однород-
ного скалярного поля
X
= (1
/
2) ˙
φ
и закон сохранения энергии запи-
сывается в виде
˙
ε
=
−
3
H
(
ε
+
p
)
,
в результате получаем уравнения
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 4
39

















