
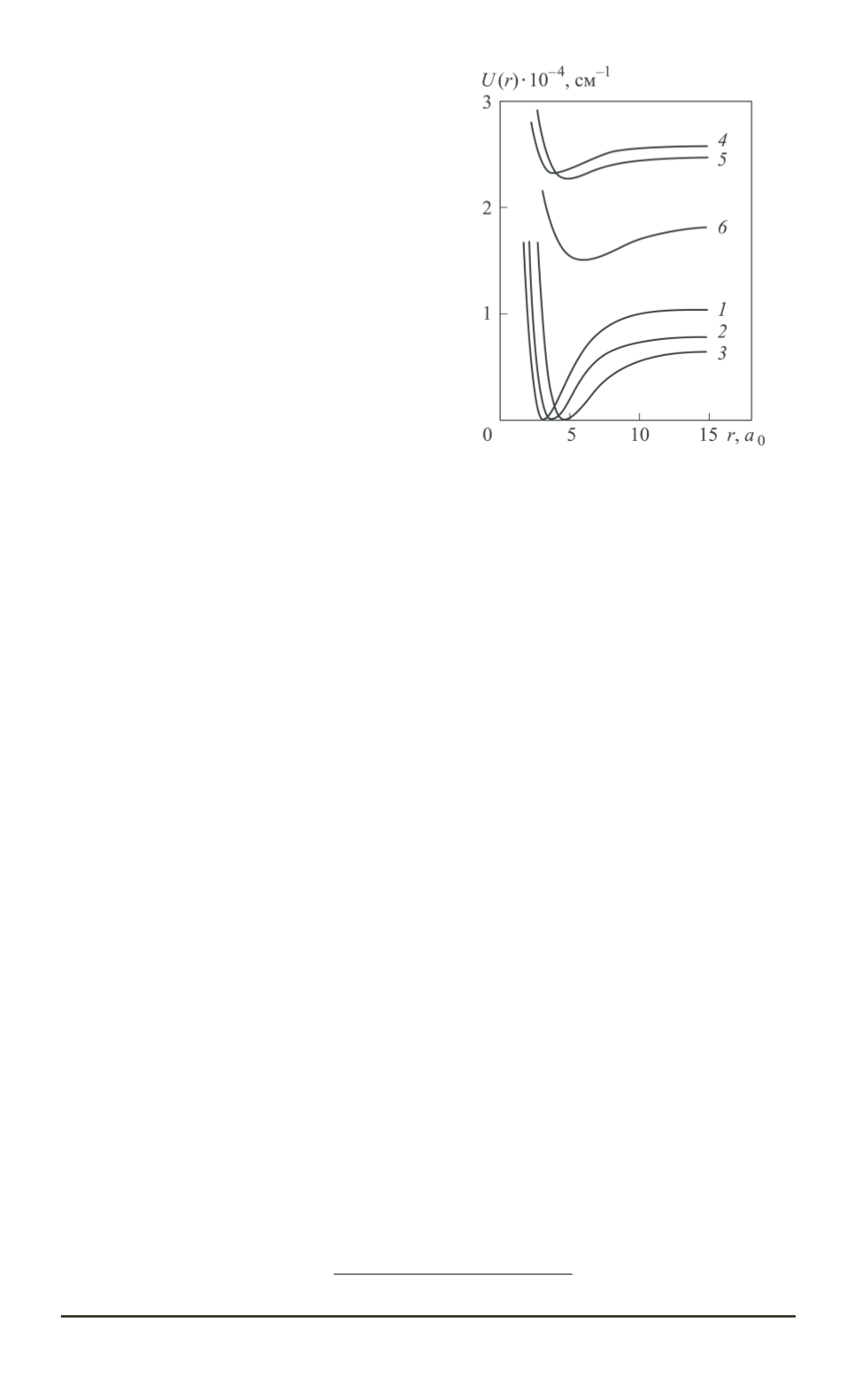
Рис. 1. Потенциальные кривые для
основных и возбужденных электрон-
ных состояний катионов димеров ли-
тия, натрия и калия:
X
2
Σ
+
g
состояние:
1
— Li
+
2
;
2
— Na
+
2
;
3
— K
+
2
;
(1)
2
Π
u
состояние:
4
— Li
+
2
;
5
—
Na
+
2
;
6
— K
+
2
колебательных квантовых чисел.
Для основных электронных состо-
яний:
v
max
(Li
+
2
) = 64
, энергия
максимально рассчитанного коле-
бательного уровня составляет 94%
значения экспериментальной энер-
гии диссоциации;
v
max
(Na
+
2
) = 74
(81%);
v
max
(K
+
2
) = 88
(76%). Для
возбужденных электронных состо-
яний колебательные энергии рас-
считаны для
v
max
= 25
. Расчет
вращательных и центробежных по-
стоянных проведен по теории воз-
мущений для модели вращающего-
ся осциллятора двухатомной моле-
кулы [21].
Вычисленные на основе потен-
циальных кривых колебательные
энергии, вращательные и центро-
бежные постоянные для основных
и возбужденных состояний аппроксимированы степенными функция-
ми, параметры которых являются молекулярными постоянными
E
ν
=
ω
e
(
v
+ 0
,
5)
−
ω
e
x
e
(
v
+ 0
,
5)
2
+
. . .
;
B
v
=
B
e
−
α
e
(
v
+ 0
,
5) +
γ
e
(
v
+ 0
,
5)
2
+
. . .
;
D
v
=
D
e
−
β
e
(
v
+ 0
,
5) +
δ
e
(
v
+ 0
,
5)
2
+
. . .
;
H
v
=
H
e
−
ξ
e
((
v
+ 0
,
5) +
ε
e
(
v
+ 0
,
5)
2
+
. . .
Молекулярные постоянные для основных и возбужденных элек-
тронных состояний катионов димеров лития, натрия и калия, полу-
ченные из оптимальных аппроксимирующих функций, приведены в
табл. 1 и сравниваются с литературными данными. Рассчитанные зна-
чения частот колебаний для основных и возбужденных состояний от-
личаются от имеющихся данных не более чем на 0,1%. Вращательные
постоянные для основных состояний различаются менее чем на 0,2%,
для возбужденных — на 0,004%. Найденные с помощью потенциаль-
ных кривых значения вращательного параметра
α
e
, центробежных по-
стоянных
D
e
и
H
e
, отсутствующие в литературе, сопоставлены со
значениями, вычисленными с использованием данных, которые опре-
делены по следующим эмпирическим соотношениям:
соотношение Пекериса [20]
α
e
=
6
B
2
e
(
ω
e
x
e
/B
e
)
1
/
2
−
1
ω
e
;
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 4
47

















