
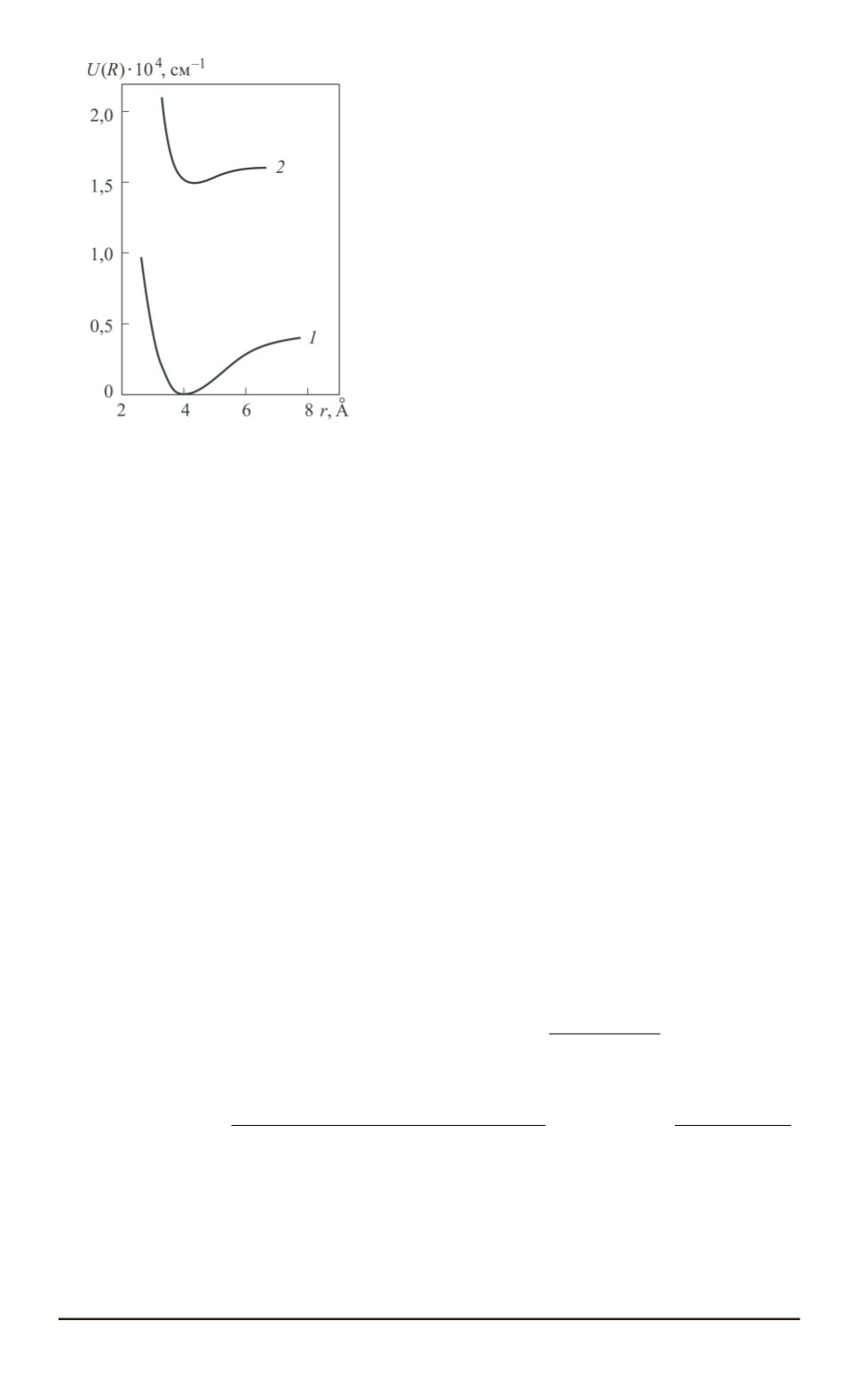
Рис. 1. Потенциальные кривые
для основного
X
1
Σ
+
(
1
) и возбу-
жденного
B
1
Π
(
2
) электронных со-
стояний молекулы KRb
прилегающей к диссоциационному
пределу молекулы, применялся по-
тенциал обменного взаимодействия
Δ
U
обм
(
R
) =
BR
α
exp(
−
βR
)
,
(2)
где
B
,
α
,
β
— параметры потенциала.
Полный набор параметров функ-
ций ВМ, РКР, (1) и (2) для основно-
го электронного состояния молекулы
KRb приведен в работе [8]. Для возбу-
жденного состояния также рассчита-
ны параметры для функций ВМ, РКР
и (1). Поворотные точки кривой РКР
электронного состояния
B
1
Π
опреде-
лены для колебательных квантовых
чисел
v
= 0
. . .
15
. Различные участки
потенциальных кривых для основно-
го и возбужденного состояний (функций ВМ, РКР и (1)) гладко сши-
вались в единую кривую. Интерполяция потенциальных кривых РКР
между поворотными точками проводилась кубическими сплайнами.
Потенциальные кривые для основного и возбужденного состояний,
построенные по рассчитанным параметрам, приведены на рис. 1.
Для проверки надежности построенных потенциальных кривых на
их основе были вычислены колебательные энергии, вращательные и
центробежные постоянные. Колебательные энергии найдены путем
численного решения радиального волнового уравнения на основе по-
тенциальных кривых, построенных в настоящей работе. Вращатель-
ные и центробежные постоянные для основного и возбужденного со-
стояний были определены по выражениям, полученным с помощью
теории возмущений для модели вращающего осциллятора двухатом-
ной молекулы [21]:
B
v
=
β v R
−
2
|
v
;
D
v
=
β
2
X
u
6
=
v
h
u
|
R
−
2
|
v
i
2
(
E
u
−
E
v
)
;
H
v
=
β
3
X
t
6
=
v
X
u
6
=
v
h
v
|
R
−
2
|
u
i h
u
|
R
−
2
|
t
ih
t
|
R
−
2
|
v
i
(
E
u
−
E
v
) (
E
t
−
E
v
)
−
β
2
B
v
X
u
6
=
v
h
u
|
R
−
2
|
v
i
2
(
E
u
−
E
v
)
2
.
Здесь
h
u
|
R
−
2
|
v
i
=
∞
Z
0
ψ
u
(
R
)
R
−
2
ψ
v
(
R
)
dR
— матричный элемент. Рас-
считанные и экспериментальные значения колебательных энергий и
54
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
















