
the developed dependences which determine the angular position of the outgoing jets
describe the numerical calculations in the range between the incoming jets from 90
to 110 degrees better than the other models. To increase accuracy in calculating the
angular position of the internal outgoing jet, we developed the dependence based
on approximating the results of the numerical calculations. The research is of great
interest to experts, who work on behavior of technological errors in cumulative
streams. The received results can be useful to specialists in jet equipment and in
explosive bonding.
Keywords
:
jets impact, outgoing jets, stationary stage of jets interaction, errors in
numerical calculations, approximating curve.
Рассмотрим установившуюся стадию соударения двух плоских
струй идеальной жидкости со свободными границами. Струи дви-
жутся под углом
2
α < π
друг к другу с одинаковой скоростью
U
и
имеют ширину
δ
1
и
δ
2
, причем
δ
1
> δ
2
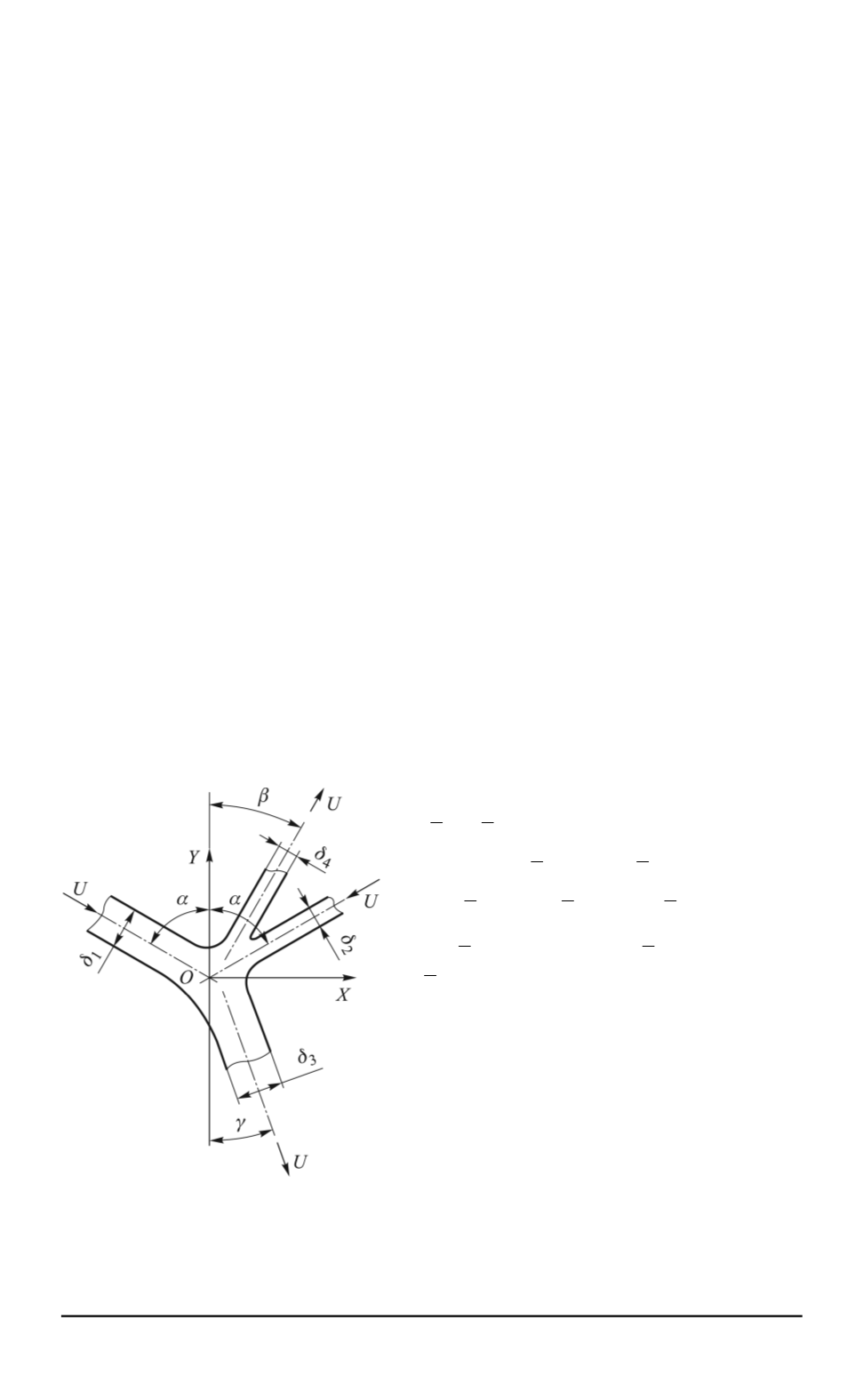
(рис. 1). Расходящиеся от места
соударения со скоростью
U
струи характеризуются следующими па-
раметрами: внутренняя струя, т.е. струя, движущаяся внутри угла
2
α
,
имеет ширину
δ
4
и отклоняется на угол
β
от оси
OY
; внешняя струя
шириной
δ
3
и угловым отклонением
γ
от оси
OY
. Одна из классиче-
ских задач теории струй идеальной жидкости предлагает определить
параметры
δ
3
,
δ
4
,
β
,
γ
расходящихся струй при известных значениях
параметров
α
,
δ
1
и
δ
2
соударяющихся струй [1]. Параметры сталкива-
ющихся и расходящихся струй определены на бесконечном удалении
от точки
О
(см. рис. 1).
В общем случае такая задача не имеет однозначного решения,
поскольку для нахождения четырех неизвестных величин можно
Рис. 1. Схема столкновения двух
плоских струй идеальной жидко-
сти со свободными границами
записать только три независимых
уравнения, основанных на законах со-
хранения массы и импульса [1]:
δ
3
+
δ
4
= 2;
2 cos
α
=
δ
3
cos
γ
−
δ
4
cos
β
;
2
4
δ
sin
α
=
δ
3
sin
γ
+
δ
4
sin
β,
(1)
где
δ
3
=
δ
3
/δ
0
;
δ
4
=
δ
4
/δ
0
;
4
δ
=
4
δ/δ
0
;
δ
0
= (
δ
1
+
δ
2
)
/
2
;
4
δ
=
= (
δ
1
−
δ
2
)
/
2
— отклонение шири-
ны соударяющихся струй от среднего
значения
δ
0
.
Задача (1) решается без привлече-
ния дополнительных условий только
в двух частных случаях [1, 2].
1. При соударении одинаковых
струй шириной
δ
1
=
δ
2
=
δ
0
и
4
δ
= 0
имеет место симметричная конфигу-
рация струй, т.е.
β
=
γ
= 0
. Решением
80
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 2
















