
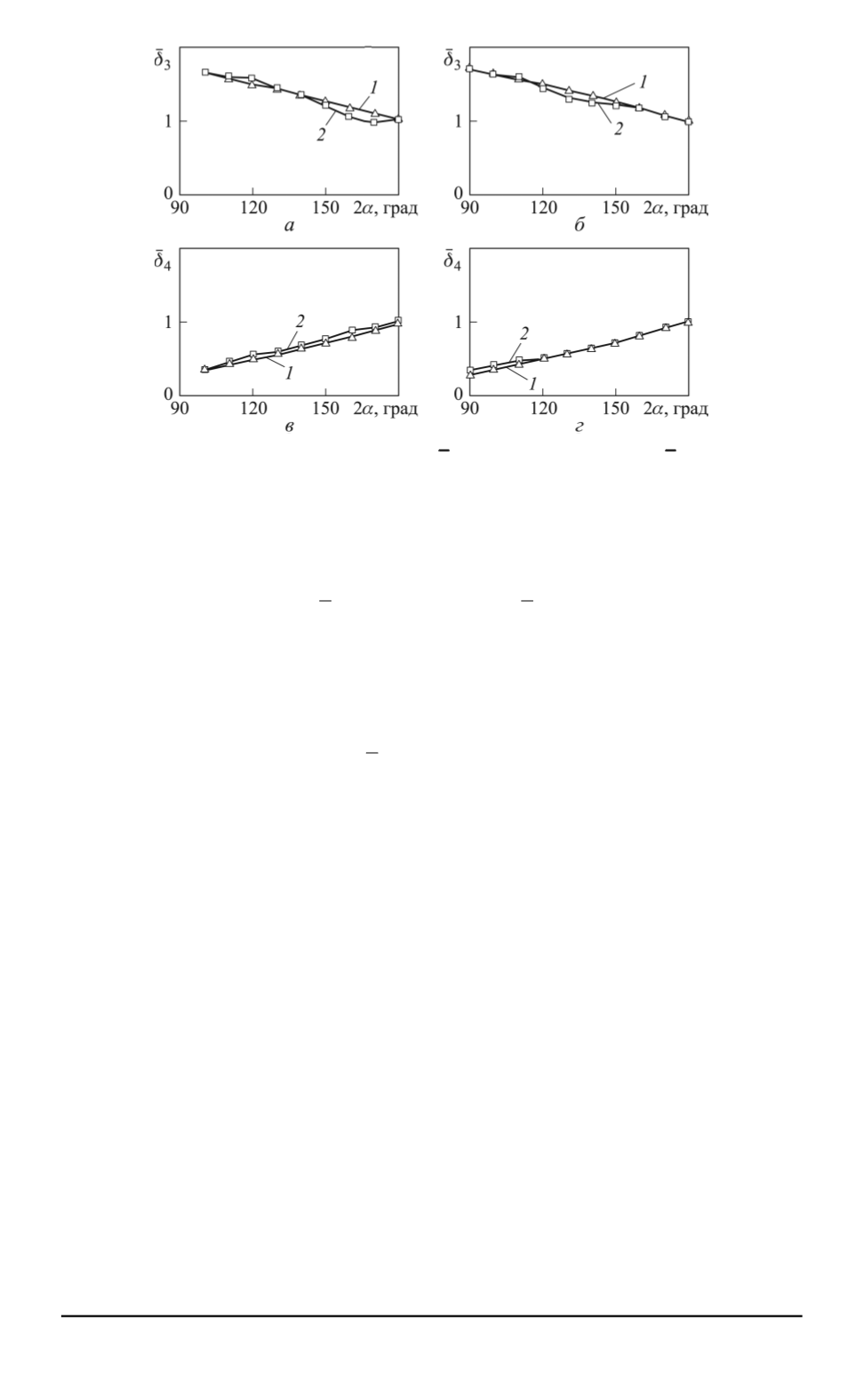
Рис. 3. Зависимости ширины внешней
δ
3
(
а, б
) и внутренней
δ
4
(
в, г
) струй
от угла
α
между соударяющимися струями, полученные по формуле (2) (
1
), и
численные зависимости (
2
) при
k
= 0
,
5
(
а
,
в
),
k
= 0
,
85
(
б
,
г
)
Проведено сравнение результатов численных расчетов ширины
расходящихся струй с предложенной в статье моделью неизменно-
сти размеров внешней
(
δ
3
)
и внутренней
(
δ
4
)
струй при переходе от
симметричного к несимметричному соударению (рис. 3).
Анализ полученных результатов позволяет сделать вывод о том,
что сделанное в настоящей статье допущение о возможности исполь-
зования зависимостей (2) для оценки ширины расходящихся струй
приемлемо не только при
4
δ
1
, но и при значительных отличиях
габаритных размеров соударяющихся струй.
Проведено сравнение результатов численных расчетов угловых от-
клонений внутренней
β
=
β
(
α
)
отходящей струи (кривая
2
, рис. 4)
с расчетами, полученными по разработанной модели (9) и по моделям
(7), (8) (кривые
1
,
3
,
4
, рис. 4). Расчеты для внешней струи
γ
=
γ
(
α
)
удовлетворительно совпадают между собой и в статье не приведены.
Анализ кривых, приведенных на рис. 4, показывает, что при
k
= 0
,
85
расчетные результаты, выполненные по различным моделям,
близки. Однако при больших различиях в ширине соударяющихся
струй (например, при
k
= 0
,
5
) наблюдаются не только существенные
расхождения расчетов, но и заметны противоречивые тенденции в ха-
рактере изменения кривых
β
=
β
(
α
)
в различных моделях (например,
кривые
3
,
4
, рис. 4,
а
) имеют кривизну разного знака). В целом можно
отметить, что в диапазоне значений углов
2
α
120
◦
. . .
180
◦
в наиболь-
шей степени результатам численных расчетов соответствует модель
(8). Однако в диапазоне значений
90
◦
. . .
110
◦
лучшее совпадение с
численными расчетами показывает разработанная модель (9).
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 2
85
















