
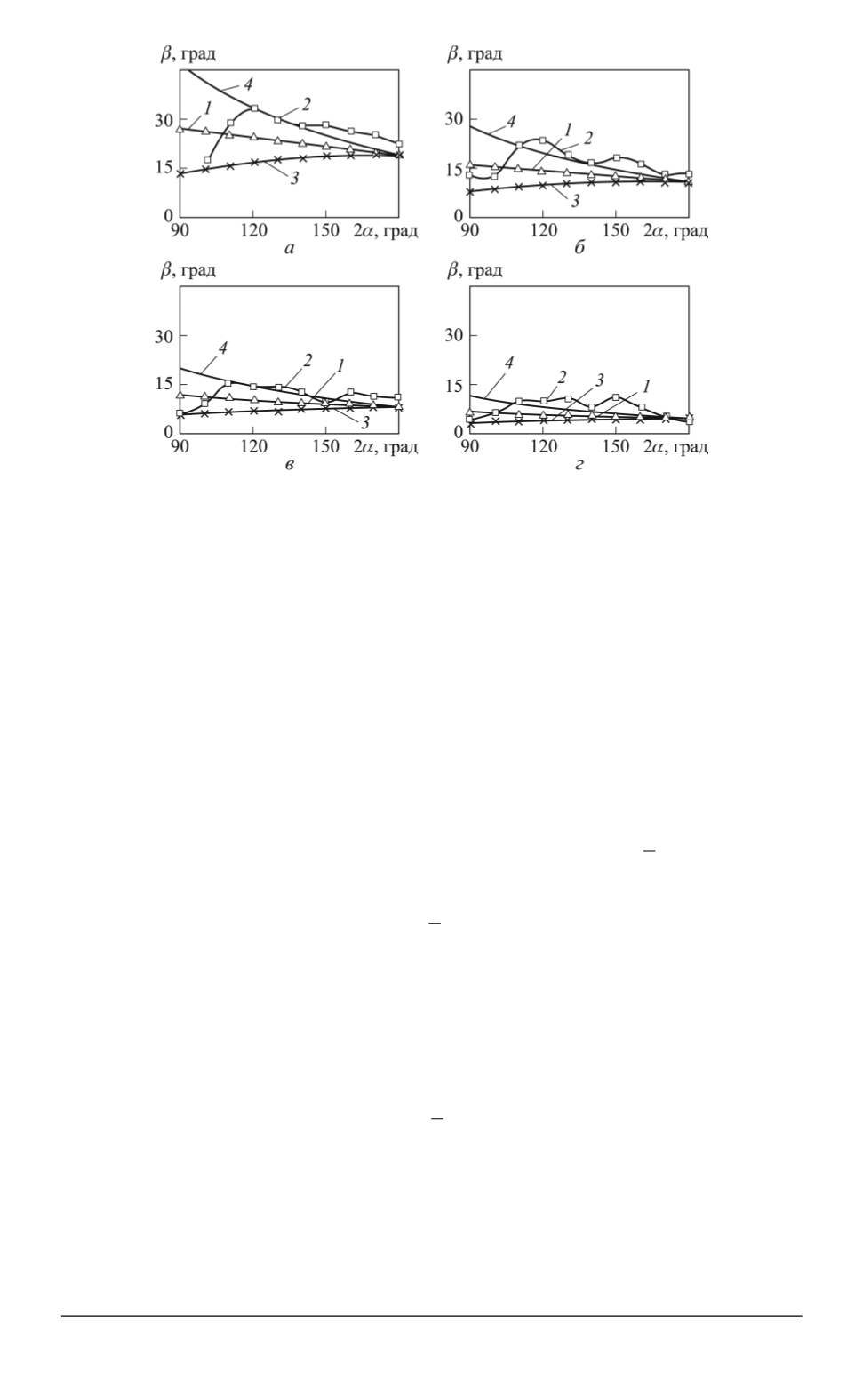
Рис. 4. Зависимости углового отклонения
β
внутренней струи от угла 2
α
между
соударяющимися струями при
k
= 0
,
5
(
а
),
k
= 0
,
667
(
б
),
k
= 0
,
75
(
в
),
k
= 0
,
85
(
г
),
полученные по (9) (
1
), (7) (
3
) и (8) (
4
), и для
β
=
β
(
α
)
отходящей струи (
2
)
Следует учесть погрешности численных расчетов при оценке угло-
вого отклонения
β
. Так, при
2
α
= 180
◦
численные расчеты должны
соответствовать данным, полученным по зависимости (3), а также по
моделям (7)–(9) (см. рис. 4). Имеющее место несовпадение результа-
тов вычислений позволяет судить о наличии случайных погрешностей,
связанных с неточностями измерений углового отклонения
β
при рас-
четных стационарных течениях плоских струй (см. рис. 2,
б
). Для ком-
пенсации этих погрешностей можно предложить следующий подход.
Разработанная модель (9) и аналитические модели (7), (8) указыва-
ют на пропорциональность между величинами
β
и
4
δ
; примем, что
пропорциональность должна соблюдаться и при численных расчетах:
β
=
4
δf
(
α
)
.
(10)
Функцию
f
(
α
)
можно получить, обрабатывая результаты числен-
ных расчетов. Численные значения функции
f
(
α
)
представим в ви-
де границ доверительных интервалов шириной 4
σ
(рис. 5), где
σ
—
среднеквадратическое отклонение значений
f
(
α
)
, полученных по ре-
зультатам численных расчетов для фиксированных значений
α
и раз-
личных значений погрешности
4
δ
. Аппроксимирующая численные
расчеты кривая (см. рис. 5)
f
(
α
) = 6(2
α
)
10
e
−
4
,
43(2
α
)
(11)
проходит внутри доверительных интервалов и может применяться со-
вместно с формулой (10) для оценки углового отклонения внутренней
86
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 2
















