
Models for Technology Programmes within an Intellectual Property…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 6
137
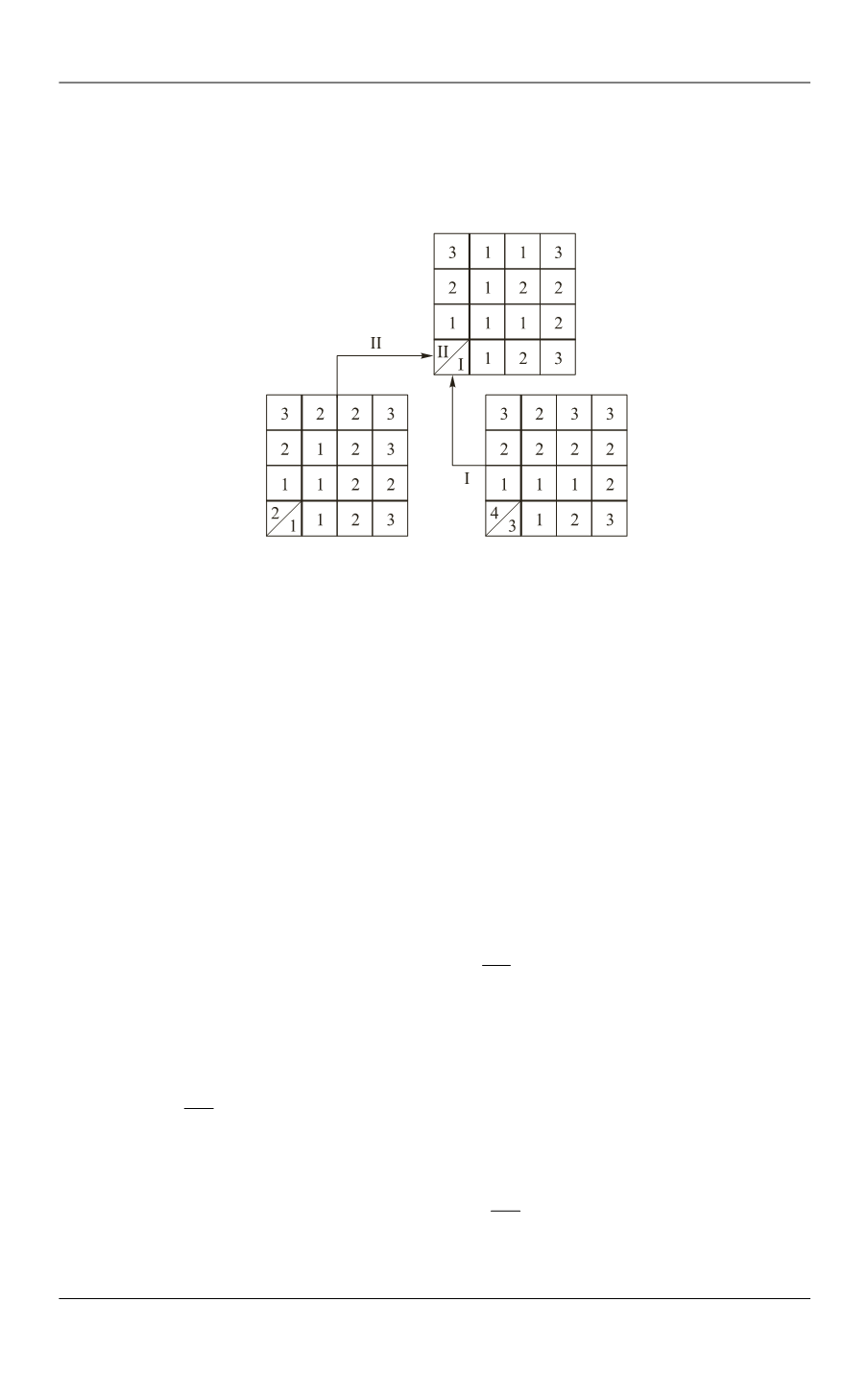
(2; 1), the total score will be 2, and if we do a reverse assessment (1; 2), it will be equal
to 1. Likewise, for directions (3; 2) the total score will be 3, and for directions (2; 3), it
is 2. For the lower right matrix direction 4 has the priority, and for the upper one,
both combined directions I and II have the same priority (a symmetric matrix).
Fig. 2.
Example of comprehensive scoring for four areas
We also need to note that the number of levels in the scoring scale can be in-
creased. This does not affect targets to be set in building a technological development
programme and the ways to achieve them. The comprehensive score of the technolo-
gy’s RL is the principal criterion when developing such programmes.
Content-wise, what we need to do is to develop a technological development pro-
gramme that would deliver the required RL, i. e. the required comprehensive score at
minimum costs over a given period of time subject to risks.
As noted by some authors, there have been some cases in Russian research prac-
tice and industrial organisations when research programmes were built within an IP
management system based on existing RIA owned by such organisations [7,8].
In such case, we would only examine the third level in the structure shown in
Fig. 1. We will not specify the level index further on. Let’s have a look at the problem
without taking risks into account. We have
n
j
projects that can be included in the
technological development programme, and
1, ,
j
m
where
m
is the number of areas.
We will first consider the programme’s scope and decide how to determine it, i. e.
which current projects are eligible to be included in the programme. As noted above,
each project i has implementation costs
i
c
and research level
w
i
. Let
x
ij
= 1, if project
i
from area
j
is included in the programme; otherwise,
x
ij
= 0. With given
,
,
1, ,
ij
j
x i Q j
m
we can determine the increase in the RL of each area
j
ij ij
i
x w
and, accordingly, the change in the score for each area, and, consequently, the change
in the comprehensive score.
Then we need to determine
,
,
1, ,
ij
j
x i Q j
m
that would deliver the required
comprehensive score at minimum costs.
















