
Models for Technology Programmes within an Intellectual Property…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 6
141
Step 1.
Take the lower left matrix. Add the second number to matrix boxes:
costs
s
1
j
and
s
2
j
(Table 6).
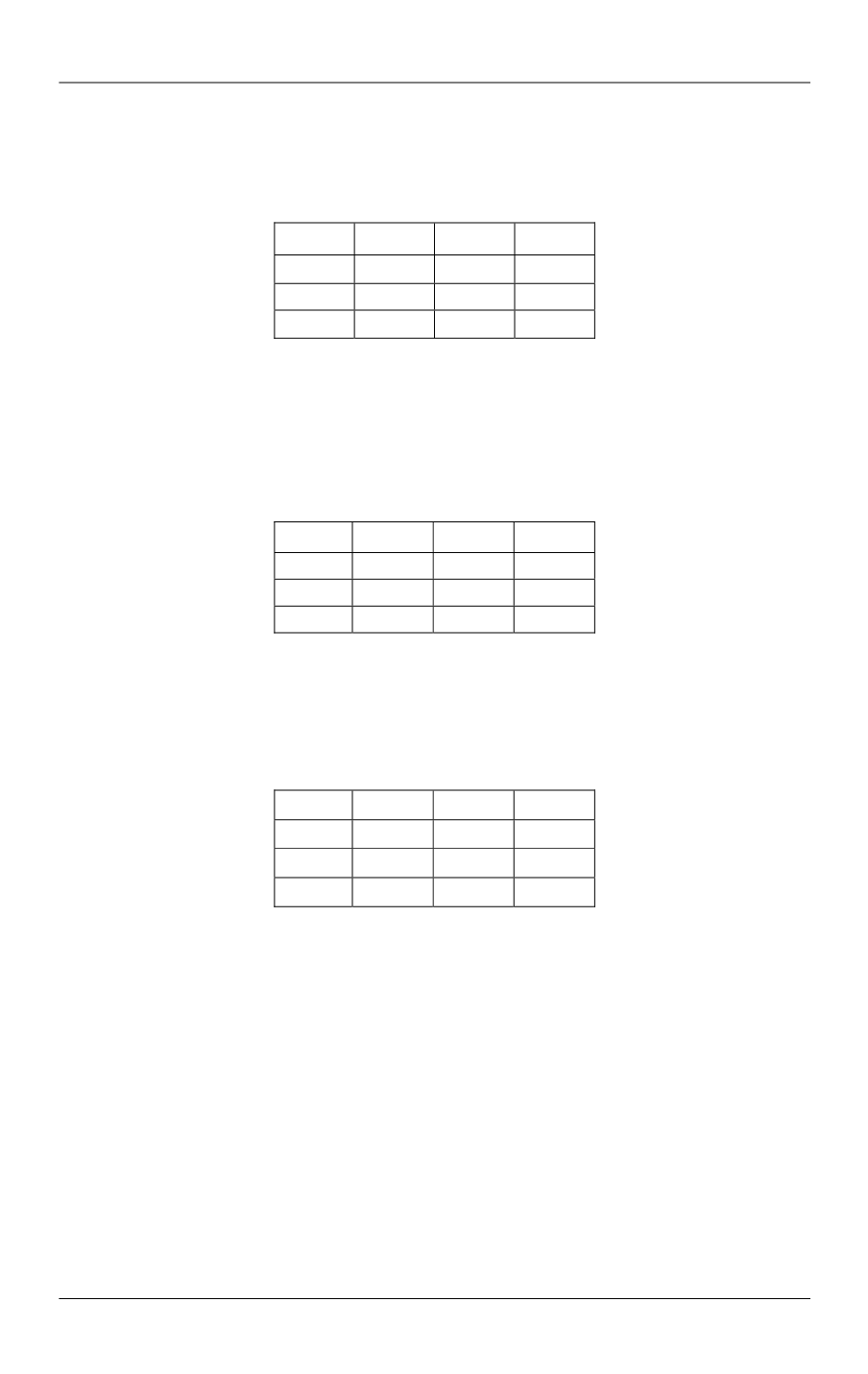
Table 6
The lower left matrix
(3; 20)
(2; 25)
(2; 36)
(3; 45)
(2; 10)
(1; 15)
(2; 26)
(3; 35)
(1; 4)
(1; 9)
(2; 20)
(2; 29)
2 / 1
(1; 5)
(2; 16)
(3; 25)
The principal rule of optimisation: choose the box with the lowest second number
out of all boxes with the same first number. The result is:
s
II1
= 9;
s
II2
= 20;
s
II3
= 35.
Step 2.
Take the lower right matrix (Table 7).
Table 7
The lower right matrix
(3; 18)
(2; 25)
(3; 31)
(3; 39)
(2; 9)
(2; 16)
(2; 22)
(2; 30)
(1; 3)
(1; 10)
(1; 16)
(2; 24)
4/3
(1; 7)
(2; 13)
(3; 21)
The result is:
s
I1
= 10;
s
I2
= 16;
s
I3
= 31.
Step 3.
Take the upper matrix (Table 8). The result is:
s
1
= 19;
s
2
= 36;
s
3
= 66.
Table 8
The upper matrix
(3; 35)
(2; 45)
(2; 51)
(3; 66)
(2; 20)
(1; 30)
(2; 36)
(2; 51)
(1; 9) (1; 19) (1; 25) (2; 40)
II / I
(1; 10) (2; 16) (3; 31)
Note that to get comprehensive score 2, we need 36 units of costs. The relevant
option of the programme, i. e. the required RL scores for each area are also deter-
mined using the backward algorithm. The optimal option corresponds to box (2; 36)
of Step 3, i. e. box (2; 16) of Step 2 and box (2; 20) of Step 1. In their turn, these boxes
correspond to score 2 for the first area, 1 for the second area, 1 for the third area, and
2 for the fourth area.
Thus, in this case the optimal strategy is to upgrade areas 1 and 4 to the global
level. To get comprehensive score 3 we need 66 units, which corresponds to score 2
for the first area, score 3 for the second area, score 2 for the third area, and score 3 for
the fourth area.
Conclusion.
The conclusion that we can draw here is that by modelling its tech-
nology development programmes an organisation is able to drastically cut down its
















