Modification of the LS-STAG Immersed Boundary Method for Simulating Turbulent Flows

13 / 16

Modification of the LS-STAG Immersed Boundary Method for Simulating Turbulent Flows
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5 31
End of Table 4
Turbulence model Number
of cells
Re 1000= Re 3900=
D C St D C St
Smag., LES, CS = 0.1 [17], ANSYS 388 550 1.15 0.21 1.07 –
Smag., LES,  max = , = 0.2,
S C
present study 71 040 1.35 0.24 1.11 0.26
Smag., LES,  max = , = 0.5,
S C
present study 71 040 1.37 0.25 1.10 0.25
S-A, RANS, present study 71 040 1.37 0.25 1.13 0.25
S-A, DES, = 0.7,
S C present study 71 040 1.37 0.25 1.11 0.25
  , k RANS, present study 71 040 1.36 0.25 1.23 0.28
  , k LES,   max = , = 0.9,
S C present
study 71 040 1.37 0.25 1.11 0.25
  , k RANS, present study 71 040 1.32 0.24 1.18 0.24
  , k DES, =1.0,
S C present study 71 040 1.32 0.25 1.00 0,25
k   SST, RANS, present study 71 040 1.34 0.25 1.14 0.25
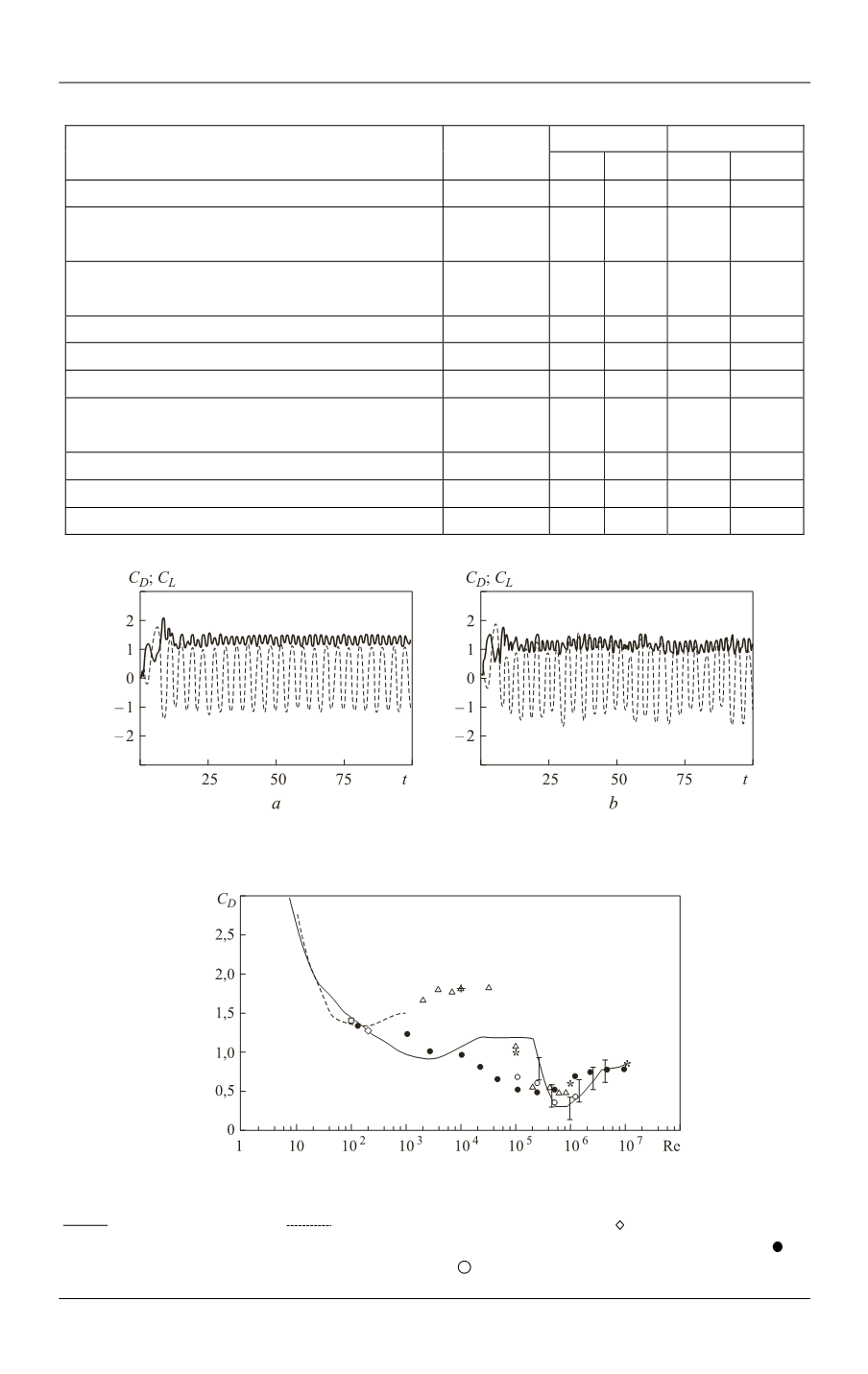
Fig. 5. Computed unsteady load ( )
D C t and ( )
L C t (RANS,   k model, mesh  240 296):
a — Re =1000 ; b — Re = 3900
Fig. 6. Comparison of the drag coefficient computed values with experimental [18]
and computational data on meshes M1–M5 [19] and [20]:
— Wieselsberger [18]; — Henderson, 2D calculations [20]; — mesh M1; + — mesh
M2; ☐ — mesh M3; × — mesh M4 with Smagorinsky model; Δ — mesh M4; * — mesh M5; —
LS-STAG (k – , RANS, 240×296); — LS-STAG (480×592)