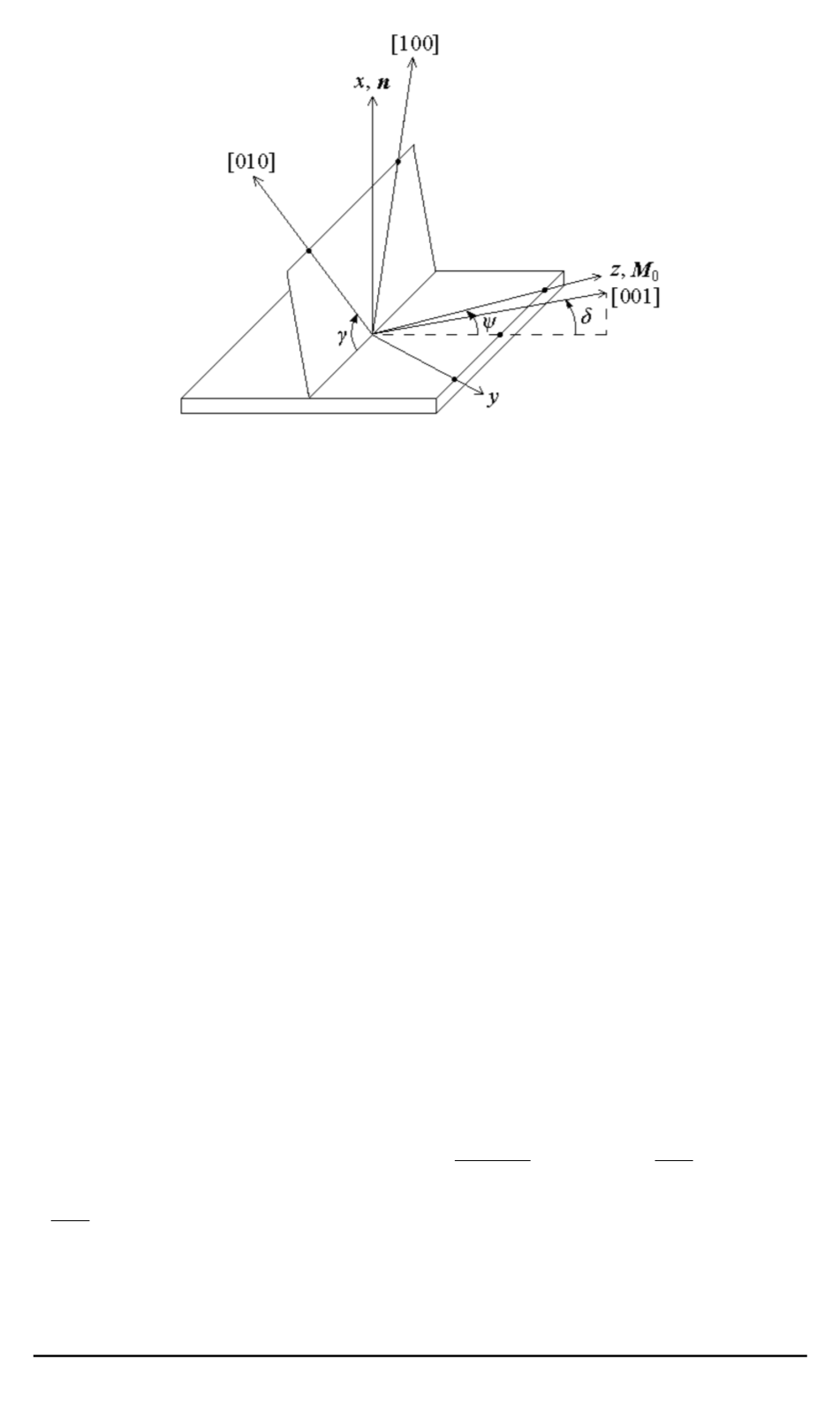
Рис. 1. Модель пленки кубического феррита при касательном намагничивании
(указаны координатные оси и кристаллографические направления,
n
— вектор
нормали к пленке)
расположенным параллельно плоскости пленки. В монокристалличе-
ской пленке, в отличие от изотропной, касательные направления не
эквивалентны друг другу и их необходимо различать. Для этого в
модель введен угол
ψ
между вектором
M
0
и проекцией на пленку
кристаллографической оси [001].
МСВ характеризуются законами дисперсии, связывающими часто-
ту
f
с волновым числом
k
. Дисперсионные уравнения (ДУ) выводят-
ся путем совместного интегрирования уравнений Максвелла, взятых
в магнитостатическом приближении и с соответствующими электро-
динамическими граничными условиями, и линеаризованного уравне-
ния движения намагниченности без учета обмена и потерь (уравнения
Ландау–Лифшица). Классификация ДУ с учетом кристаллографиче-
ской магнитной анизотропии материала пленки подробно изложена
в работе [8]. Пример спектра, рассчитанного на основе формул ра-
боты [8], приведен на рис. 2. Расчет проводили для МСВ с волно-
вым вектором, перпендикулярным вектору намагниченности пленки,
k
?
M
0
; ПМСВ, ПОМСВ, ООМСВ — поверхностные, прямые объ-
емные и обратные объемные МСВ;
f
0
— частота длинноволновой гра-
ницы спектров;
f
∞
, f
νF
, f
νB
— частоты коротковолновых границ спек-
тров ПМСВ, ПОМСВ и ООМСВ;
f
0
4
πM
0
g
2
= 1
,
f
νF
f
0
2
= 1
,
1
,
f
νB
f
0
2
= 0
,
95
. В общем случае можно выделить три частотных ин-
тервала, в каждом из которых существуют волны определенного типа
— ПМСВ, ОМСВ и ООМСВ. В отличие от ПМСВ оба типа объем-
ных волн — многомодовые (на рис. 2 изображены несколько мод с
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 3
41


