На рис. 3, 4 представлены зависимости, рассчитанные по данной
методике и на основе приведенных выше выражений для граничных
частот и компонент тензора анизотропии при
H
c
= 0
,
H
e
4
πM
0
=
1
3
,
dH
c
dT
=
−
0
,
1
d
(4
πM
0
)
dT
. На рисунках введены следующие обозначения:
α
0
=
1
f
0
df
0
dT
;
α
∞
=
1
f
∞
df
∞
dT
;
|
α
M
|
=
1
4
πM
0
d
(4
πM
0
)
dT
— нормировоч-
ный множитель. Индексы кристаллографических плоскостей, вдоль
которых ориентирована пленка, использовались для определения зна-
чений угла
δ
. Зависимости позволяют оценить масштабы изменений
ТКЧ для пленок разных кристаллографических ориентаций.
Далее рассмотрим два частных случая, которые интересны тем,
что для них расчет ТКЧ может быть выполнен точно, т.е. с учетом
производных
dH
ez
/
dT
и
dψ
/
dT
. В одном случае будем полагать
ψ
= 0
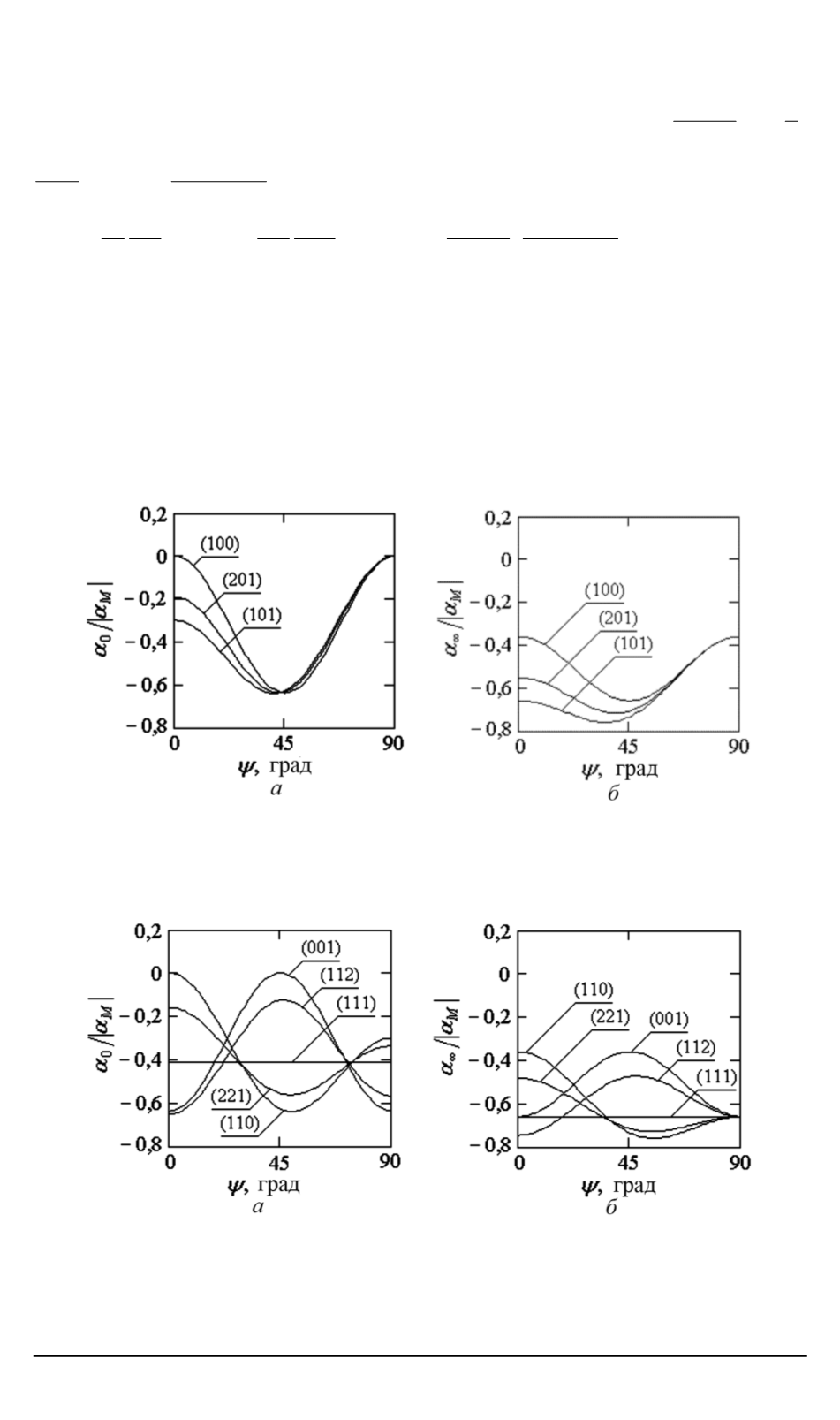
Рис. 3. Угловые зависимости ТКЧ длинноволновой (
a
) и коротковолновой (
б
)
границ спектра МСВ в касательно намагниченной пленке, ориентированной
вдоль кристаллографической плоскости (
a
0
b
)
Рис. 4. Угловые зависимости ТКЧ длинноволновой (
a
) и коротковолновой (
б
)
границ спектра МСВ в пленке, ориентированной вдоль кристаллографической
плоскости (
aab
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 3
45


