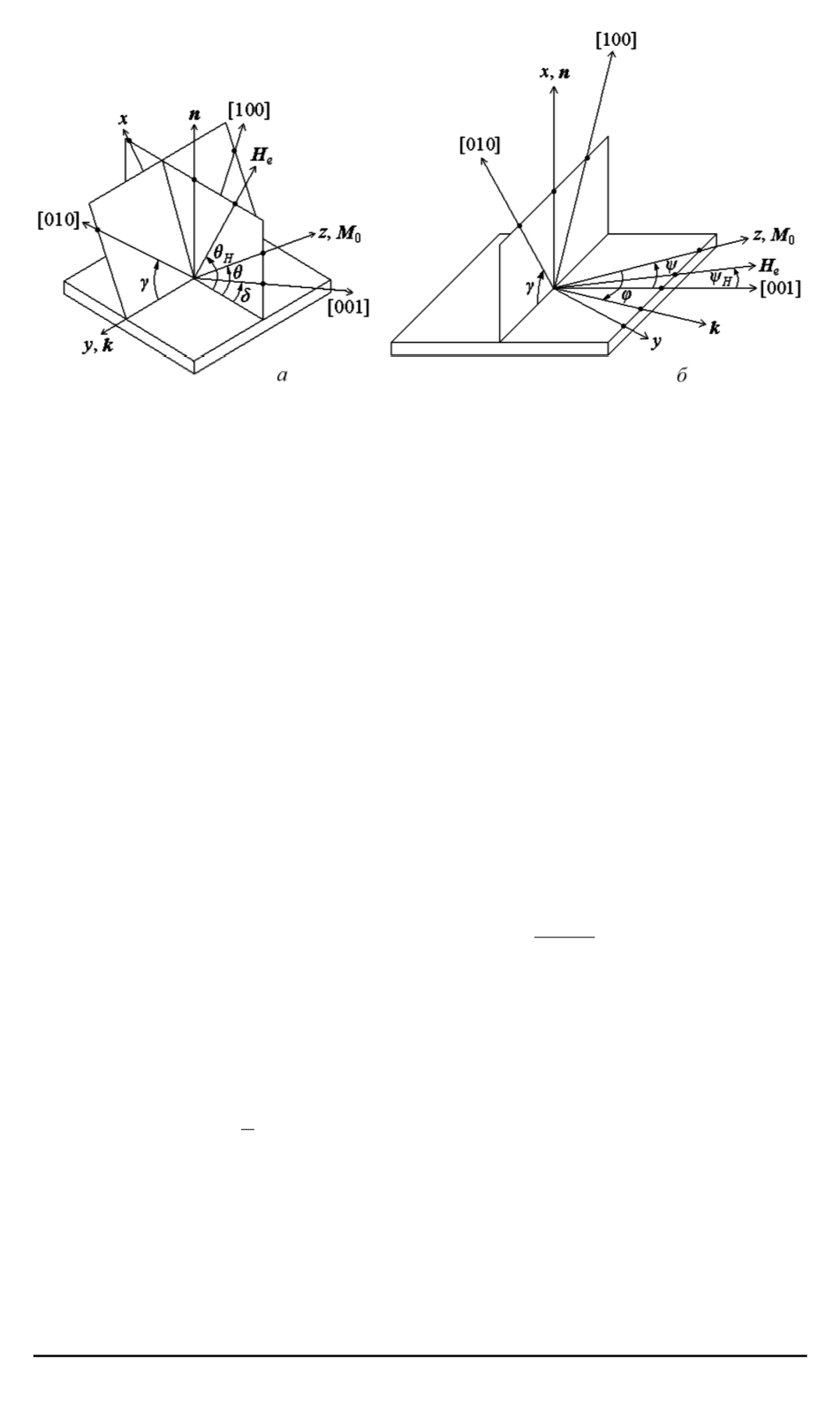
Рис. 5. Модель пленки с кристаллографическими плоскостями типа {100} или
типа {110}, расположенными перпендикулярно (
а
) или касательно (
б
) к пленке,
которая намагничена в этих плоскостях при значениях угла
γ
= 0 и
π/
4
(рис. 5,
а
), в другом —
δ
= 0
(рис. 5,
б
). В обоих случаях при
γ
= 0
вектор намагниченности
M
0
будет расположен в кристаллографиче-
ской плоскости типа {100}, а при
γ
=
π
/4
— в плоскости типа {110}.
Поскольку указанные плоскости являются плоскостями симметрии ку-
бического кристалла, вектор
M
0
будет оставаться в этих плоскостях
при любых значениях магнитных параметров пленки. Это существен-
но упрощает выполнение аналитических расчетов, так как темпера-
турное изменение ориентации вектора
M
0
можно характеризовать с
помощью только одной угловой переменной. В общем случае ориен-
тация вектора
M
0
описывается двумя угловыми переменными.
При
ψ
= 0
равновесная ориентация вектора намагниченности
определяется по уравнениям магнитостатики
H
ez
=
H
e
cos (
θ
H
−
θ
) ;
(6)
H
ex
=
H
e
sin (
θ
H
−
θ
) =
M
0
N
c
xz
+
sin 2
θ
2
∙
4
πM
0
,
(7)
где
θ
и
θ
H
— угловые переменные (см. рис. 5,
а
). В уравнении (7)
кроме кристаллографической магнитной анизотропии также учтена
анизотропия формы пленки, проявляющаяся при выходе вектора
M
0
из плоскости пленки. С учетом формулы (4) получаем
M
0
N
c
xz
=
1
8
H
c
[2
r
sin 2 (
θ
−
δ
) + (4
−
r
) sin 4 (
θ
−
δ
)]
,
(8)
где
r
= (1/2) (1
−
cos 4
γ
)
, и для значений
γ
= 0
и
γ
=
π
/4
соответ-
ствующие значения будут
r
= 0
и
r
= 1
.
Дифференцируя уравнения (6)–(8) по температуре и проводя про-
стые преобразования, получаем при
θ
= 0
(так как рассматривается
ПМСВ в условиях касательного намагничивания пленки)
46
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 3


