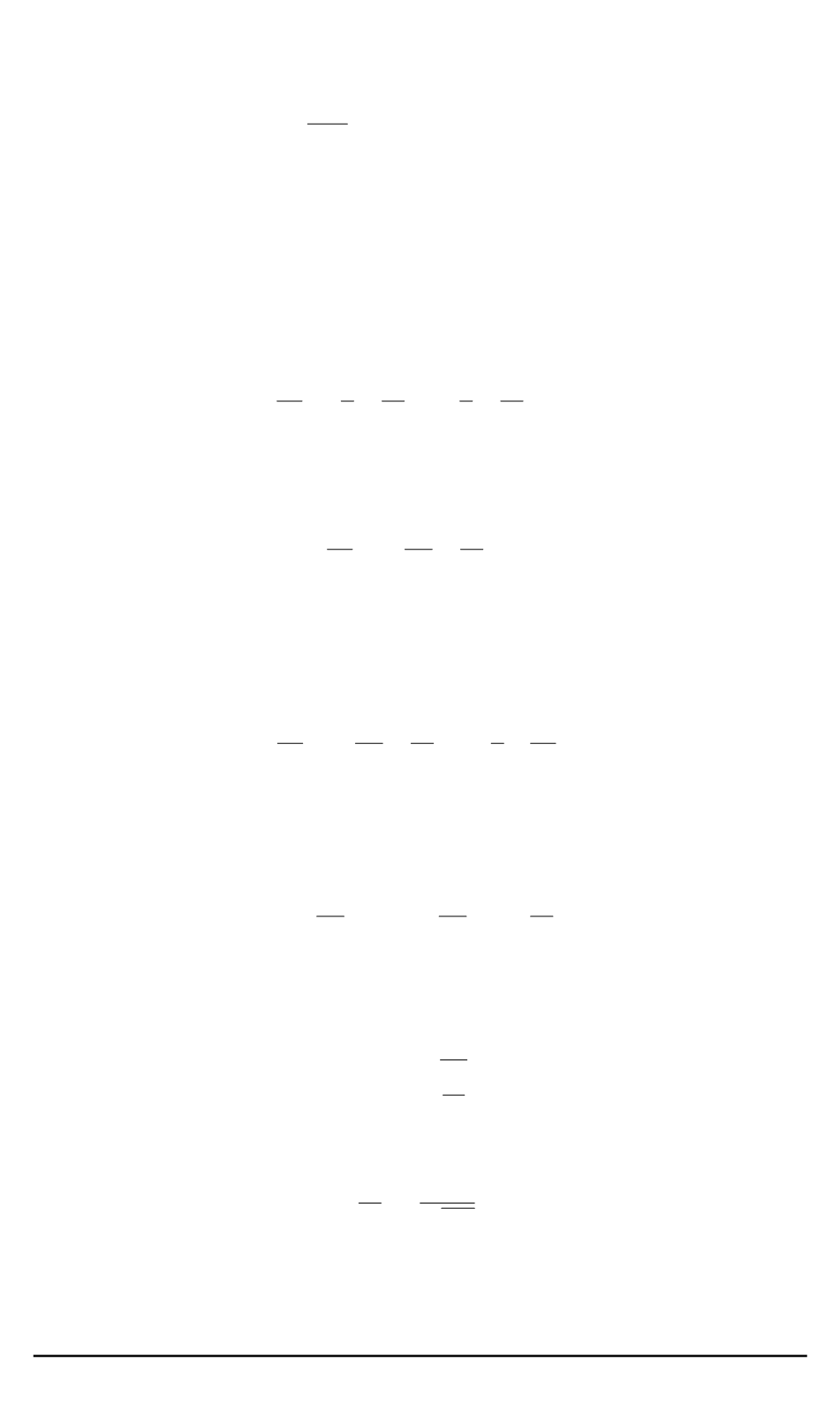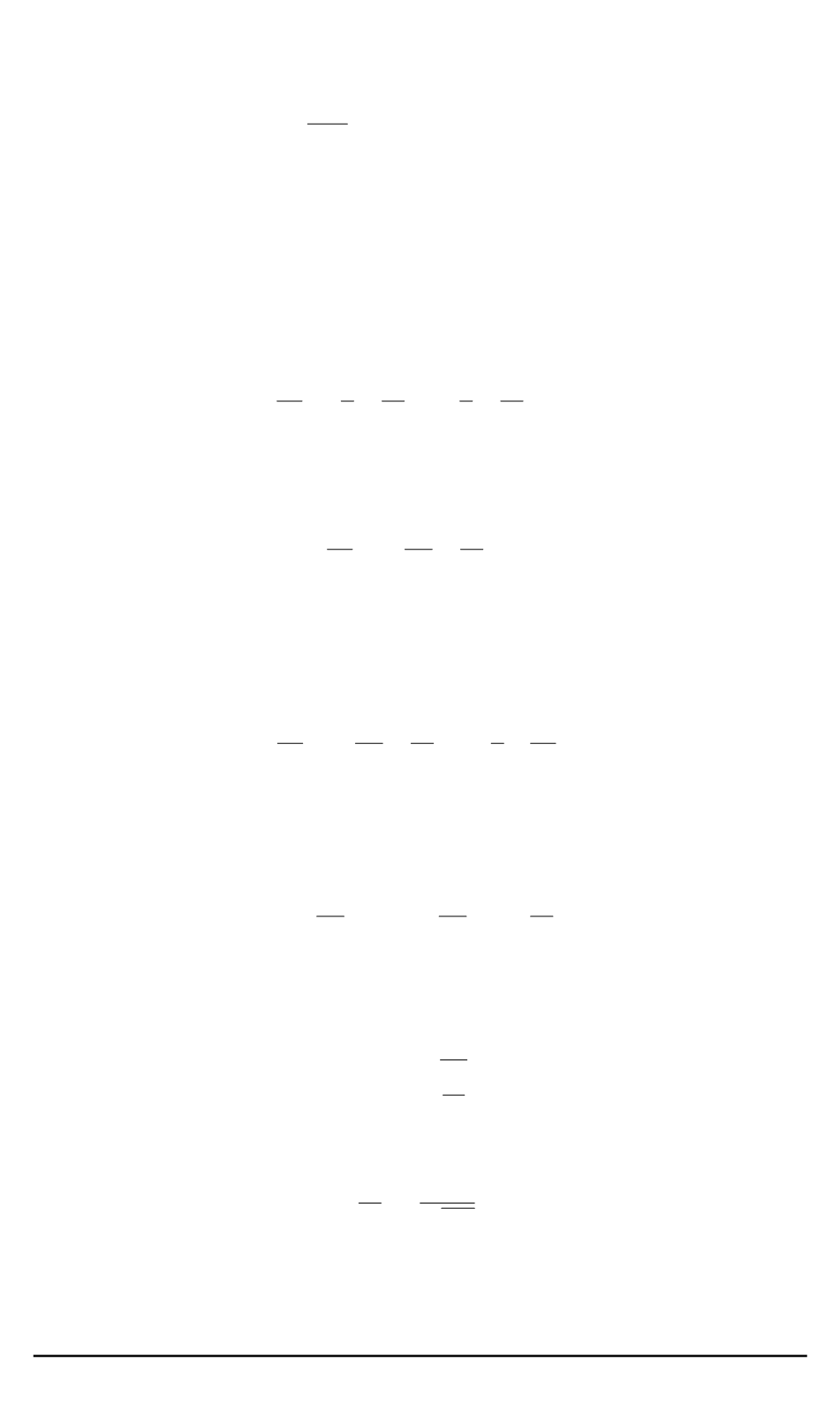
Таким образом, имеем еще одно граничное условие для границы
воздух–пластина:
∂
2
n
∂y
2
= 0
при
у
= 0
.
Приближенное решение также представим в виде полинома тре-
тьей степени
n
=
A
+
By
+
Cy
2
+
Ey
3
.
Подставив на основании этого полинома соответствующие выра-
жения в граничные условия, определим значения неизвестных коэф-
фициентов и окончательное решение примет вид
n
n
0
=
3
2
y
δ
д
−
1
2
y
δ
д
3
.
(7)
Подставим (7), а также выражение для определения скорости в
левую часть уравнения (6), проинтегрируем и получим
3
20
n
0
v
0
d
dx
δ
2
д
δ
.
При этом на основании сравнения коэффициентов переноса было учте-
но, что толщина диффузионного пограничного слоя меньше толщины
гидродинамического пограничного слоя. Теперь уравнение (6) прини-
мает вид
3
20
n
0
v
0
d
dx
δ
2
д
δ
=
3
2
D
n
0
δ
д
.
Введем следующее обозначение отношения толщины диффузион-
ного пограничного слоя к толщине гидродинамического пограничного
слоя:
k
=
δ
д
/δ
, тогда
k
3
δ
dδ
dx
+ 2
k
2
δ
2
dk
dx
= 10
D
v
0
.
Выражение для определения толщины
δ
известно из решения ин-
тегрального уравнения Кармана для пограничного слоя. В результате
интегрирования уравнения получим
k
=
3
r
D
ν
.
Если ввести безразмерный параметр, аналогичный числу Прандтля, то
δ
д
δ
=
1
√
Pr
0
.
Коэффициент диффузии меньше кинематического коэффициента
вязкости, следовательно, толщина диффузионного пограничного слоя
меньше толщины гидродинамического пограничного слоя.
102
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 3