Задача типа Стефана с произвольным числом подвижных границ фазовых превращений - page 4

Ts (x, t, χs−1 , χs ) =
=
T ∗
s−1 erf (χs) − T ∗
s erf χs−1
as−1
as
+ T ∗
s − T ∗
s−1 erf x
2√as t
erf (χs ) − erf χs−1
a s−1
as
,
x∗
s (t) < x < x ∗
s−1 (t ) , t > 0; s = 2 , n − 1; (15)
Tn (x, t, χn−1) = Tw1 − Tw1 − T ∗
n−1
erf x
2√an t
erf χn−1
an−1
an
,
0 < x < x∗
n−1 (t) , t > 0. (16)
Для определения коэффициентов χs , s = 1, n − 1, подставим ре-
шения (14)–(16) в краевые условия (4), получим систему n − 1 транс-
цендентных уравнений относительно χs , s = 1, n − 1. Не теряя общ-
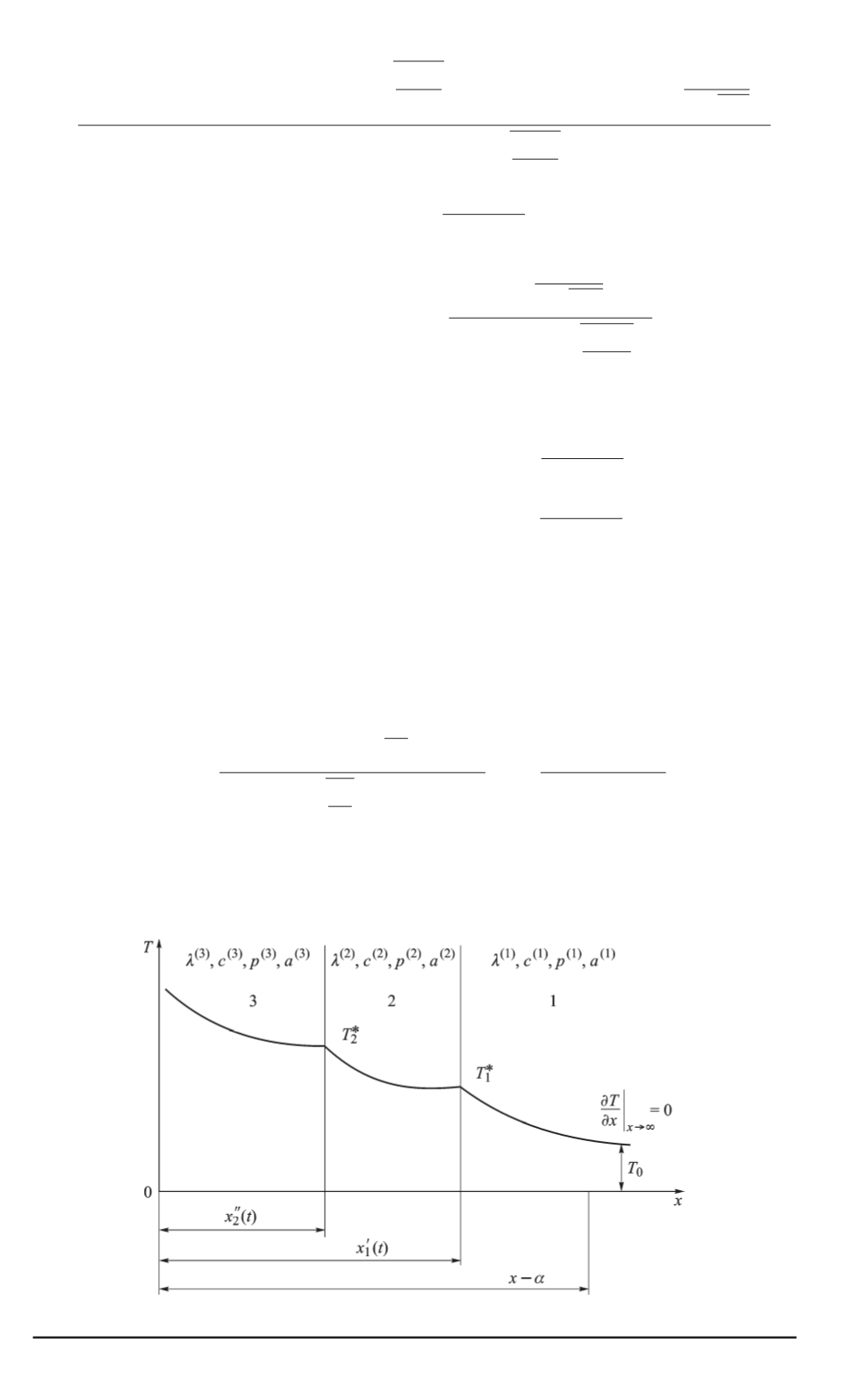
ности всего алгоритма, рассмотрим задачу (1)–(9) для n = 3 с двумя
нестационарно подвижными границами x = x∗
1 (t) и x = x∗
2 (t), для
определения координат которых получаем следующую систему двух
трансцендентных уравнений (качественная картина процесса предста-
влена на рис. 1):
FI (χ1 , χ2 ) = E
exp −χ2
1
a1
a2
erf χ 1
a1
a2 − erf (χ2 )
− F
exp (− χ2
1 )
1 − erf (χ1 ) − χ 1 = 0,
(17)
Рис. 1. Расчетная схема
52 ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 2