cm
i
=
cm
0
1 + 2
am
0
i
k
=1
(
−
1)
k
am
k
+
i
k
=1
(
−
1)
k
Δ
m
k
−
1
+ Δ
m
k
am
k
;
cn
j
=
cn
0
1 + 2
an
0
j
k
=1
(
−
1)
k
an
k
+
j
k
=1
(
−
1)
k
Δ
n
k
−
1
+ Δ
n
k
an
k
.
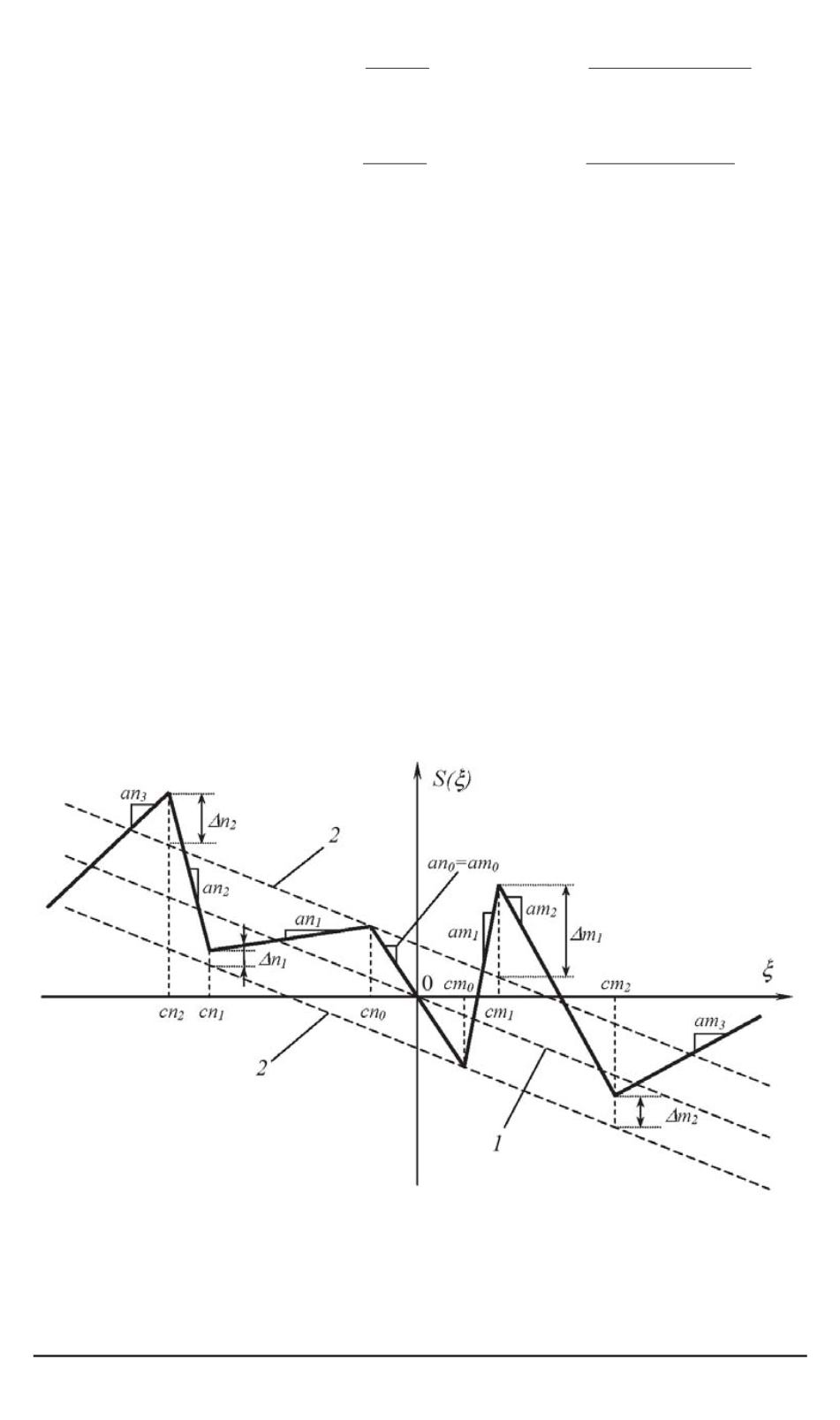
В выражении (3) коэффициенты
am
i
и
an
j
задают наклоны сег-
ментов, а коэффициенты
Δ
m
i
и
Δ
n
j
— это смещения ординат границ
сегментов относительно их положений, отвечающих случаю регуляр-
ной многосегментной нелинейности (рис. 8).
Постоянные в уравнениях (2) выбирались равными
А
= 2
,
В
= 7
,
a
=
−
4
,
b
= 2
.
Отличительной особенностью сигналов, генерируемых автостоха-
стическими системами с многосегментной нелинейностью, является,
несмотря на существенную разницу свойств используемых генерато-
ров хаоса, практически полная идентичность свойств низкочастотной
импульсной составляющей таких сигналов, которая содержит всю ин-
формацию о модулирующем сигнале. Это делает их полностью сход-
ными с наиболее широко используемыми в настоящее время носителя-
ми информации — модулированными сигналами с детерминированной
несущей.
Поэтому использование генераторов хаоса с управляемой много-
сегментной нелинейностью позволяет дополнить известные методы
Рис. 8. Многосегментная нелинейная функция с имеющими различный наклон
и длинулинейными сегментами:
1
— ось симметрии регулярной многосегментной функции;
2
— линии, на которых
расположены точки соединения ее сегментов
106
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3


