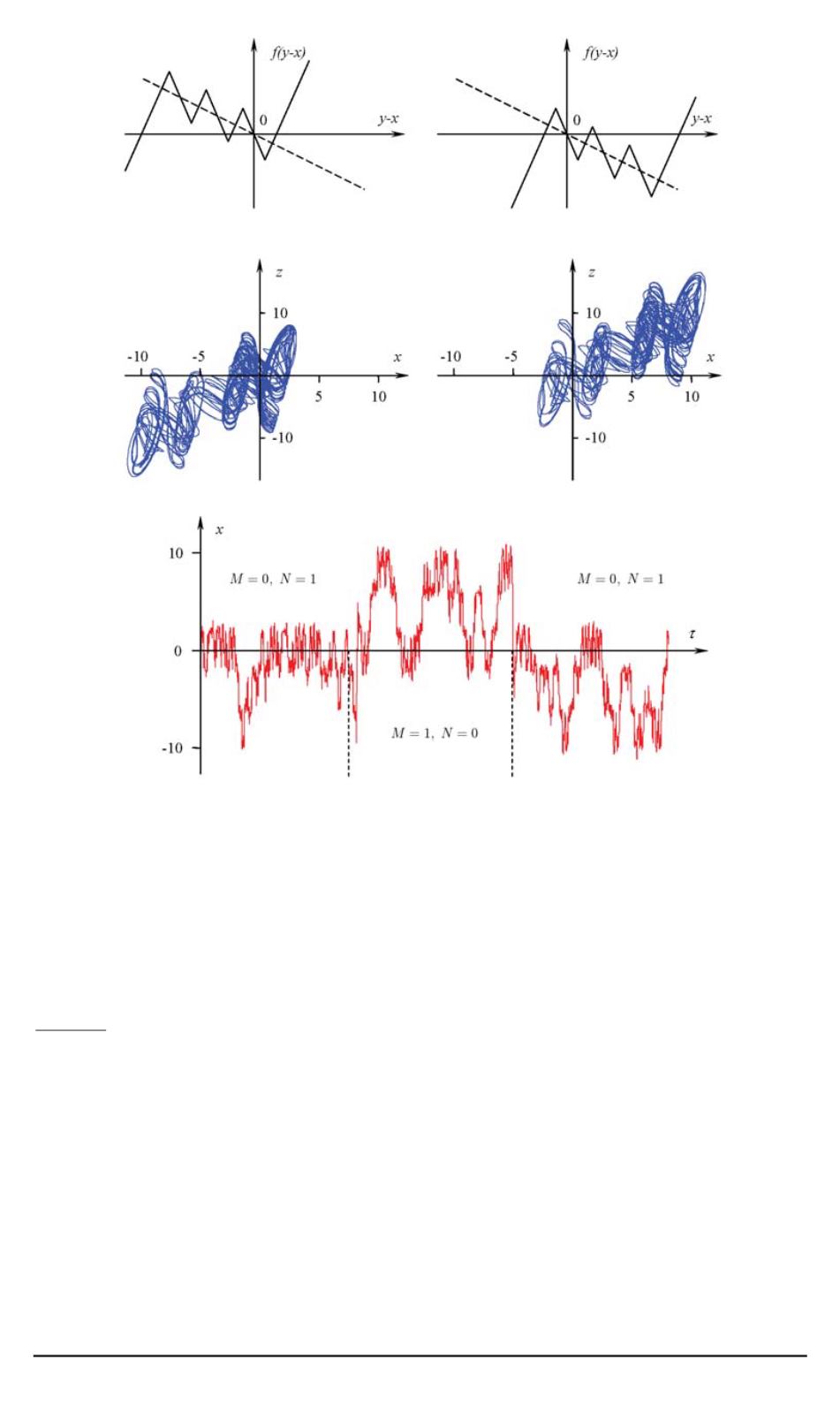
Рис. 2. Модуляция смещением нелинейной функции вдоль оси симметрии
Так как число сегментов образует ряд целых чисел, то при исполь-
зовании первого способа модулирующий сигнал должен быть дискрет-
ным. Глубина модуляции лимитируется числом сегментов в составе
нелинейной функции, которое равно
3 + 2
k
,
k
= 0
,
1
,
2
, . . .
[5]. По-
этому максимальная глубина модуляции в общем случае здесь равна
2
k
3 + 2
k
, т.е. может изменяться от 40% при
k
= 1
до 80% при
k
= 6
и (в
пределе) до 100% при неограниченном увеличении числа сегментов.
В частности, такая модуляция может осуществляться пошаговым
смещением нелинейной функции вдоль линии нагрузки. Этот способ
основан на свойстве трансляционной инвариантности режима колеба-
ний автономных динамических систем с регулярной многосегментной
нелинейностью.
При смещении такой нелинейной функции вдоль оси симметрии
на интервал
[
kc, k
с
]
, где
k
— целое число, все однотипные сегмен-
ты переходят друг в друга: сегменты с наклоном
a
в сегменты с на-
100
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3


