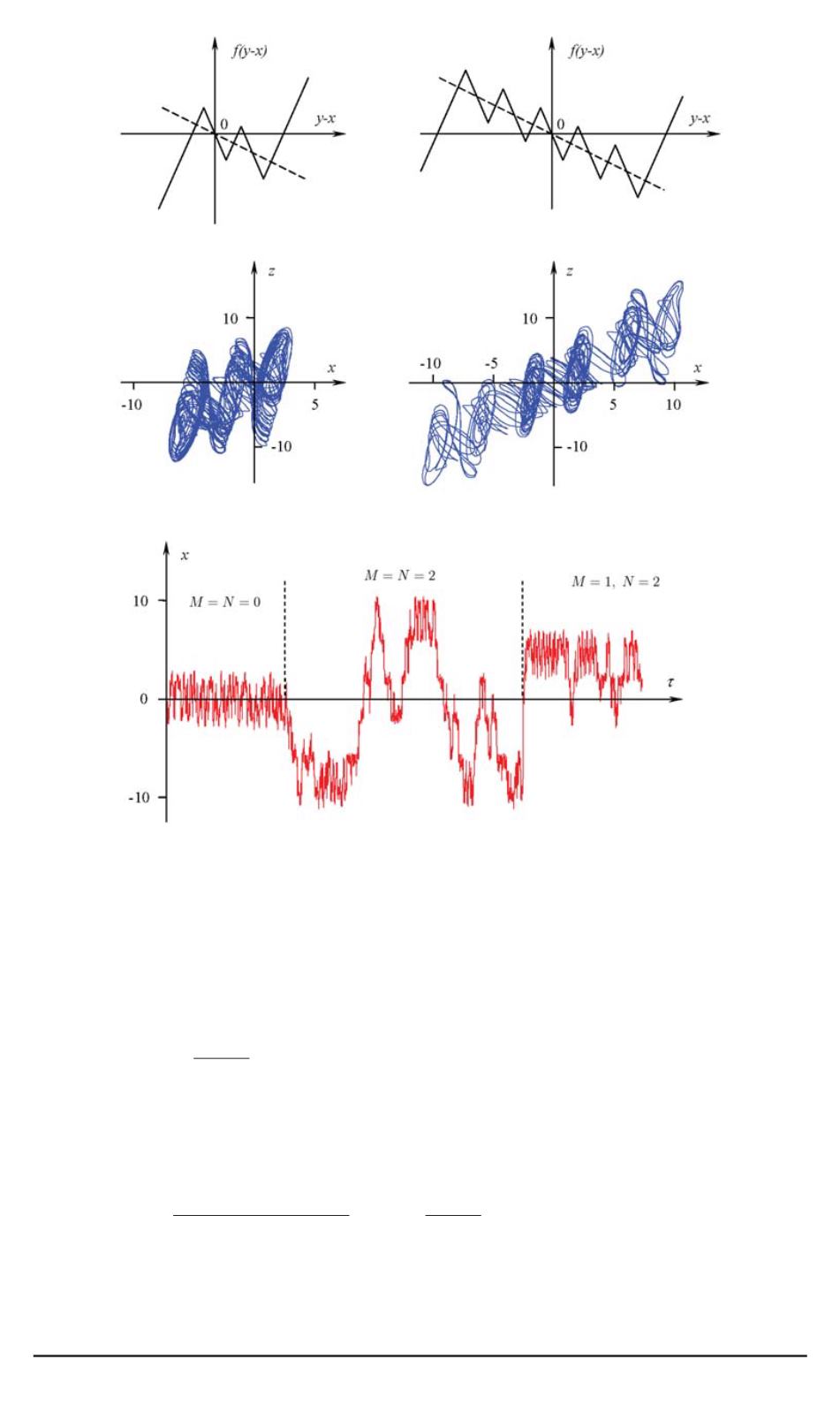
Рис. 1. Модуляция хаотического сигнала изменением числа сегментов регуляр-
ной многосегментой нелинейной функции
одинаковые интервалы (см. рис. 1). В этом случае осью симметрии
функции является прямая, пересекающая все сегменты (кроме боко-
вых) посередине. В случае линейных сегментов такую нелинейность
можно представить, например, следующим уравнением:
S
(
ξ
) =
bξ
+
a
−
b
2
−
P
(
ξ
) +
+
M
m
=1
[
P
(
ξ
+
mcγ
)
−
γ
] +
N
n
=1
[
P
(
ξ
−
ncγ
) +
γ
]
,
(1)
где
P
(
ξ
) =
|
ξ
+
γ
| − |
ξ
−
γ
|
2
;
c
= 2
a
−
b
1
−
b
. Коэффициенты
a
и
b
задают
наклон сегментов,
M
и
N
— их число, равное
3 + 2(
M
+
N
)
,
M
+
+
N
= 0
,
1
,
2
, . . .
;
γ
— масштабный коэффициент, равный единице, если
только не ставится задача вариации масштаба нелинейной функции.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3
99


