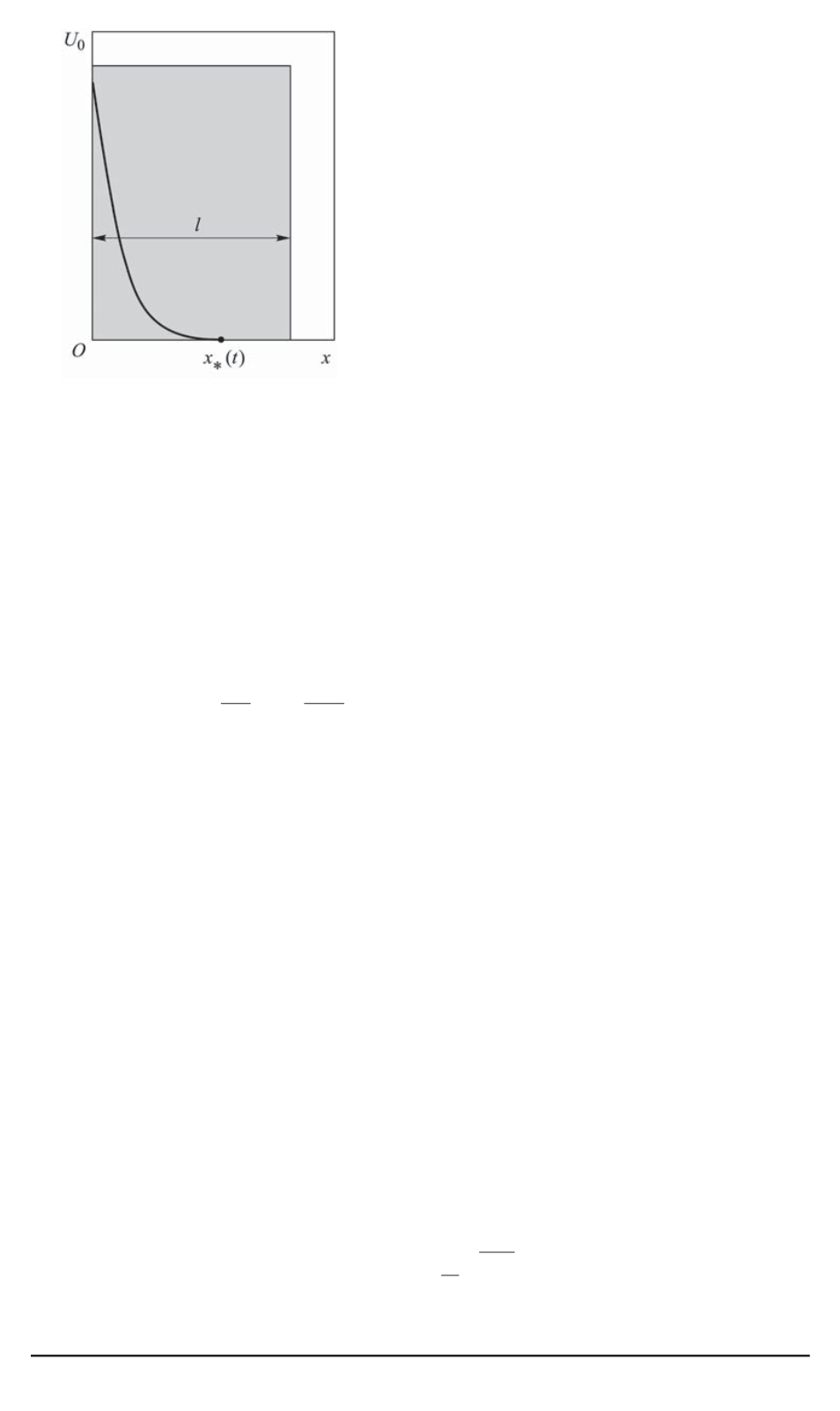
Рис. 1. Качественный вид темпе-
ратурного профиля тепловой вол-
ны в слое в фиксированный мо-
мент времени
Необходимо отметить, что в рабо-
те [2] был обоснован следующий вы-
вод: такие нелинейные эффекты мо-
гут наблюдаться и при наличии нели-
нейностей только в младших членах
квазилинейных параболических урав-
нений. Результаты настоящей работы
подтверждают этот вывод.
Физическая постановка задачи
и математическая модель процес-
са.
Рассмотрим задачу о нахождении
нестационарного температурного по-
ля
u
(
x, t
)
в плоском слое конечной
толщины
l
. В начальный момент вре-
мени (
t
= 0
) температура слоя равна
нулю. При
t >
0
на поверхности
x
= 0
этого слоя поддерживается температура
U
0
, а на поверхности
x
=
l
—
нулевая температура. Во внутренних точках слоя происходит погло-
щение теплоты, удельная мощность которой составляет
f
(
u
) =
p
0
u
α
,
где
α >
0
;
p
0
>
0
— коэффициент поглощения.
Математическая модель процесса имеет вид
ρc
∂u
∂t
=
λ
∂
2
u
∂x
2
−
p
0
u
α
,
0
< x < l, t >
0;
u
(
x,
0) = 0
,
0
< x < l
;
u
(0
, t
) =
U
0
, u
(
l, t
) = 0
, t >
0
,
(1)
где
ρ
,
c
,
λ
— плотность, удельная теплоемкость и коэффициент тепло-
проводности.
Особенность решения такого класса задач заключается в том, что
при
α <
1
наблюдаются эффекты конечной скорости и пространствен-
ной локализации возмущений. В этом случае тепловое возмущение
от нагретой поверхности
x
= 0
распространяется в виде тепловой
волны (рис. 1) с конечной скоростью перемещения ее фронта
x
∗
(
t
)
.
Кроме того, при определенных значениях параметров задачи тепловое
возмущение проникает в слой на конечную глубину и не достигает
поверхности
x
=
l
при
t
→ ∞
.
Фронт тепловой волны.
Отметим, что существует точное стаци-
онарное решение уравнения в задаче (1), которое имеет вид
u
st
(
x
) =
⎧⎨ ⎩
U
0
1
−
x
L
2
1
−
α
, x < L
;
0
, x
≥
L.
28
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 4


