x
∗
(
t
) =
b
0
b
1
(1
−
exp (
−
b
1
t
))
.
Отметим, что
b
0
/b
1
=
L
2
(значение
L
вычисляется по (2)), тогда
x
∗
(
t
) =
L
1
−
exp (
−
b
1
t
)
.
(7)
При рассматриваемых в задаче (1) значениях параметра
α
(
0
<α<
1
)
выражение
(3
−
α
)
/
(1 +
α
)
, определяющее знак постоянной
b
1
, при-
нимает положительные значения.
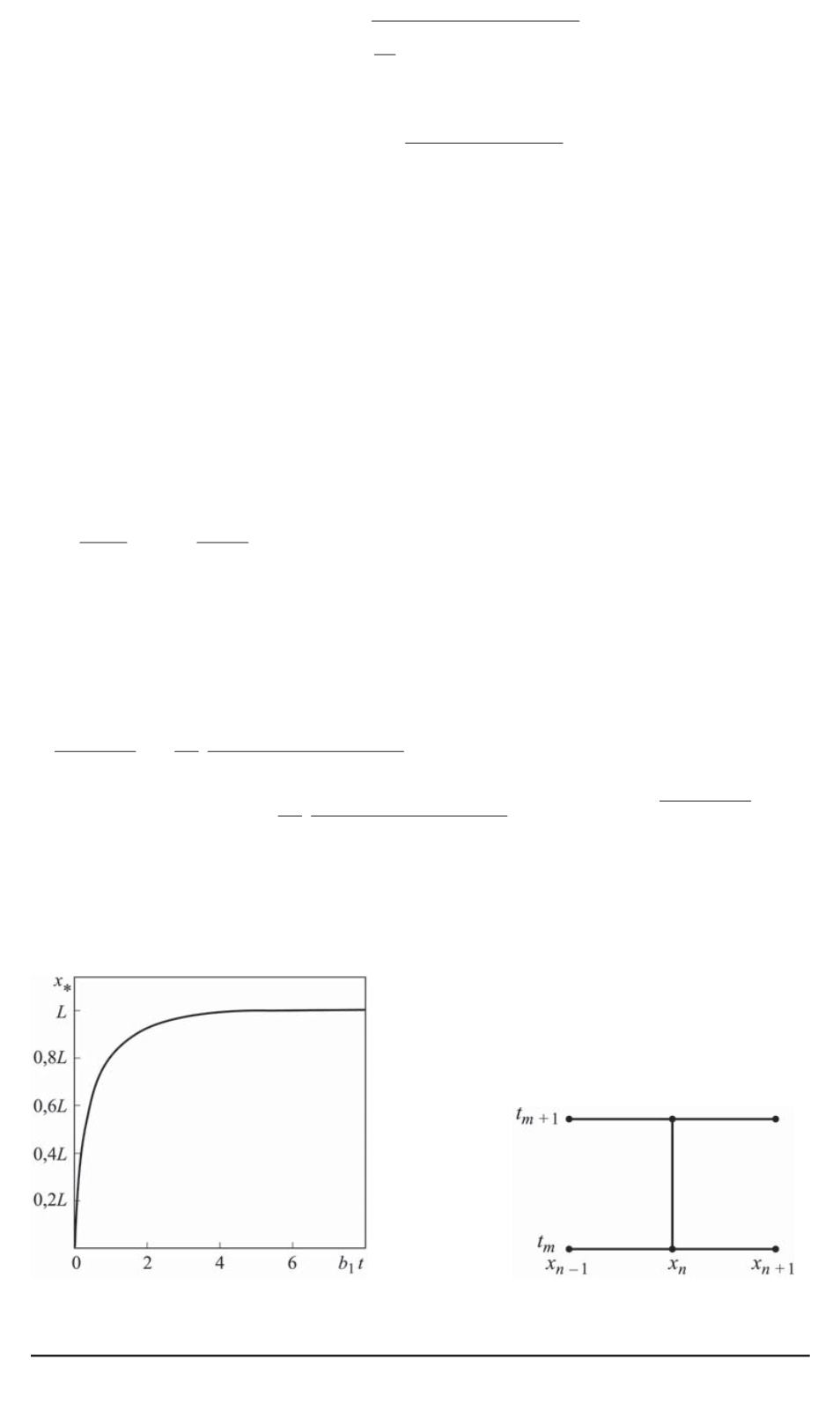
Решение (3) описывает тепловое возмущение, распространяюще-
еся в виде тепловой волны, фронт
x
∗
(
t
)
которой перемещается с ко-
нечной скоростью. Закон движения
x
∗
(
t
)
имеет вид (7) и представлен
на рис. 2. Особенность этой зависимости — при
t
→ ∞
координата
фронта
x
∗
стремится к конечному значению
L
.
Разностная схема.
Для численного решения исходной задачи ис-
пользуем разностную схему. В области
D
= [0
≤
x
≤
l
]
×
[0
≤
t
≤
T
]
зададим равномерную сетку
ω
hτ
= (
x
n
, t
m
) :
x
n
=
nh
,
t
m
=
mτ
,
n
= 0
, N
,
m
= 0
, M
с шагами
h
=
l/N
и
τ
=
T/M
по переменным
x
и
t
соответственно.
Обозначим
y
n
=
y
(
x
n
, t
m
)
, y
n
=
y
(
x
n
, t
m
+1
)
, f
n
=
f
(
y
n
)
,
f
n
=
f
(
y
n
)
и, используя шеститочечный шаблон (рис. 3), запишем
разностную схему с полусуммой [4]:
y
n
−
y
n
τ
=
a
2
2
y
n
−
1
−
2
y
n
+
y
n
+1
h
2
+
+
a
2
2
y
n
−
1
−
2
y
n
+
y
n
+1
h
2
−
f
n
,
n
= 1
, N
−
1
.
(8)
Из граничных условий находим
y
0
=
U
0
,
y
N
= 0
.
Разностная схема (8) является нелинейной. Для ее решения приме-
ним метод последовательных приближений
Рис. 2. Характер изменения поло-
жения фронта тепловой волны
Рис. 3. Шеститочечный шаб-
лон разностной схемы
30
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 4


