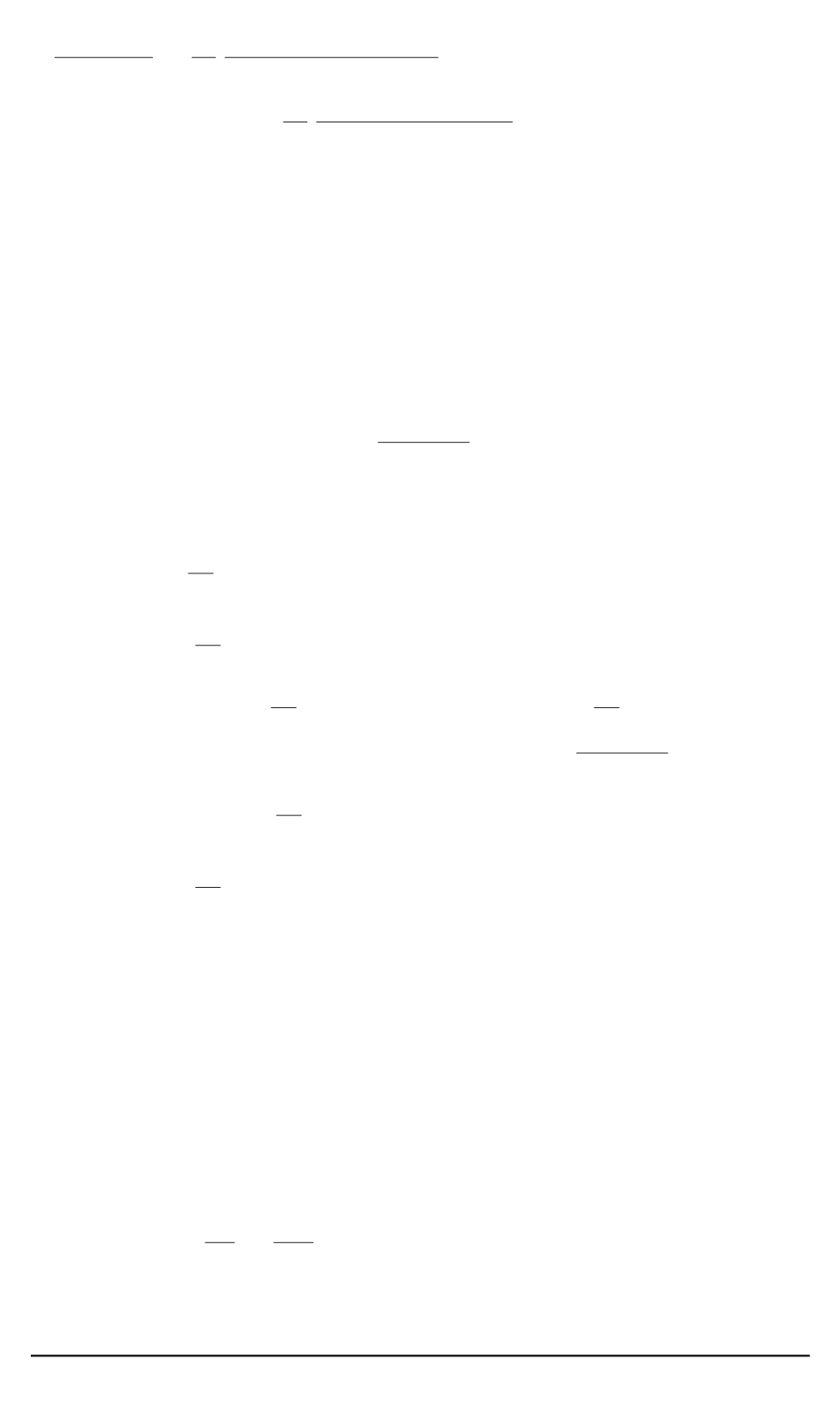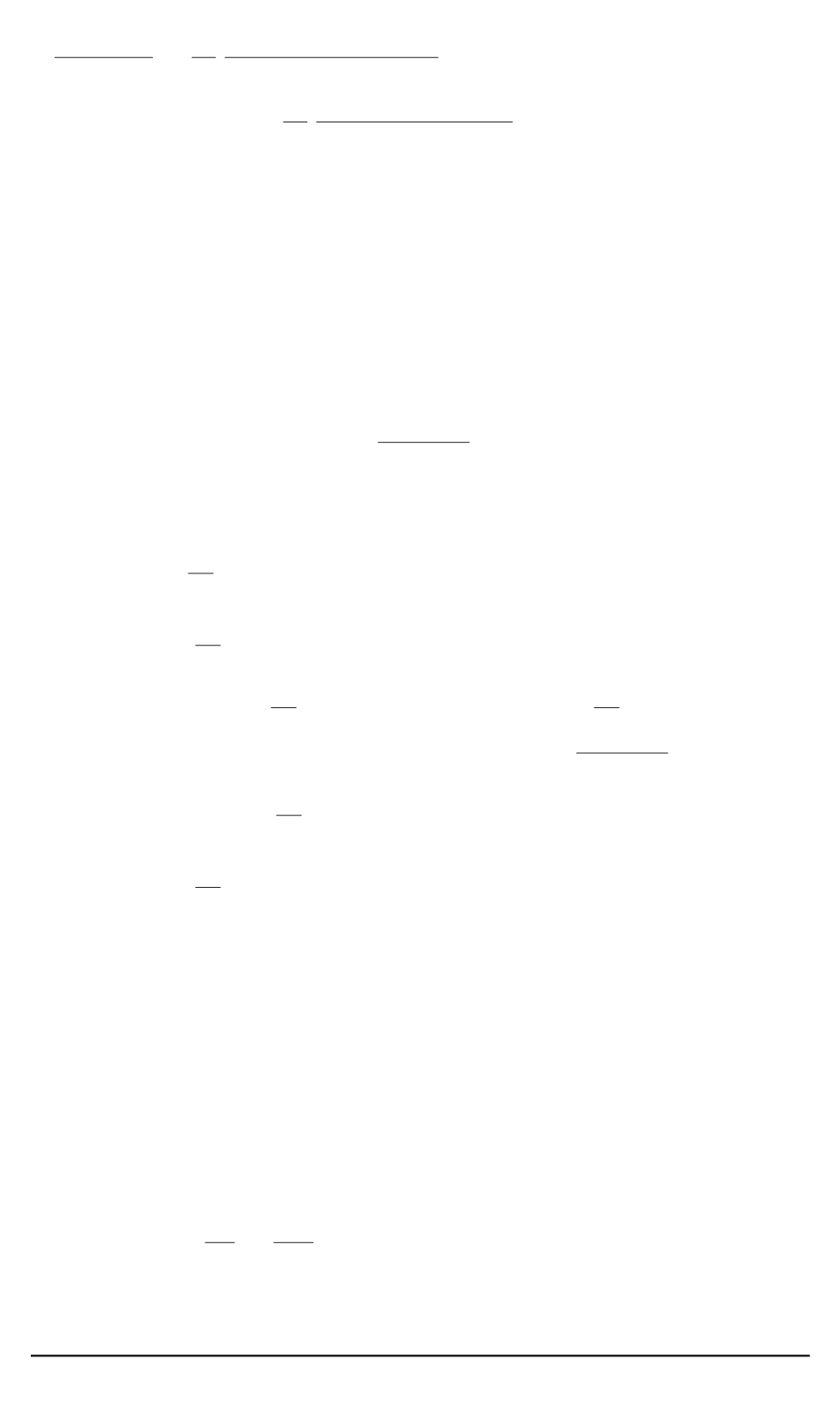
y
(
k
)
n
−
y
n
τ
=
a
2
2
y
(
k
)
n
−
1
−
2
y
(
k
)
n
+
y
(
k
)
n
+1
h
2
+
+
a
2
2
y
n
−
1
−
2
y
n
+
y
n
+1
h
2
−
f
(
k
−
1)
n
, k
= 1
,
2
, . . .
;
y
(0)
n
=
y
n
.
Опишем итерационную процедуру нахождения решения на вре-
менн´ом слое
t
m
+1
.
Шаг 1
(
k
= 1
). За нулевое приближение
f
(0)
n
принимаем значение
f
n
с предыдущего временн´ого слоя
t
m
и определяем первое прибли-
жение
y
(1)
n
решения
y
n
.
Шаг 2
(
k
= 2
). Используя значение
y
(1)
n
, вычисляем
f
(1)
n
=
f y
(1)
n
,
а затем — второе приближение
y
(2)
n
решения
y
n
и т.д.
Шаг
k
. Величины
y
(
k
)
n
,
n
= 1
, N
−
1
, могут быть найдены методом
прогонки из решения трехдиагональной системы линейных алгебраи-
ческих уравнений
−
2
a
2
+
h
2
τ
y
(
k
)
1
+
a
2
y
(
k
)
2
=
= 2
a
2
−
h
2
τ
y
1
−
a
2
(
y
0
+
y
2
) + 2
h
2
f
(
k
−
1)
1
−
a
2
y
(
k
)
0
;
a
2
y
(
k
)
n
−
1
−
2
a
2
+
h
2
τ
y
(
k
)
n
+
a
2
y
(
k
)
n
+1
= 2
a
2
−
h
2
τ
y
n
−
−
a
2
(
y
n
−
1
+
y
n
+1
) + 2
h
2
f
(
k
−
1)
n
, n
= 2
, N
−
2;
a
2
y
(
k
)
N
−
2
−
2
a
2
+
h
2
τ
y
(
k
)
N
−
1
=
= 2
a
2
−
h
2
τ
y
N
−
1
−
a
2
(
y
N
−
2
+
y
N
) + 2
h
2
f
(
k
−
1)
N
−
1
−
a
2
y
(
k
)
N
.
(9)
Элементы матрицы системы (9) удовлетворяют условиям диаго-
нального преобладания, которые являются достаточными условиями
того, что в формулах для определения прогоночных коэффициентов
ни один из знаменателей не обращается в нуль, а обратная прогонка
устойчива по входным данным [5].
Для выбора значений шагов
h
и
τ
может быть применена методика,
изложенная в работе [6].
Пример численного расчета.
Приведем результаты численного
расчета для задачи вида
∂u
∂t
=
∂
2
u
∂x
2
−
48
u
1
/
2
,
0
< x <
1
, t >
0;
u
(
x,
0) = 0
,
0
< x <
1;
u
(0
, t
) = 1
, u
(1
, t
) = 0
, t >
0
.
(10)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 4
31