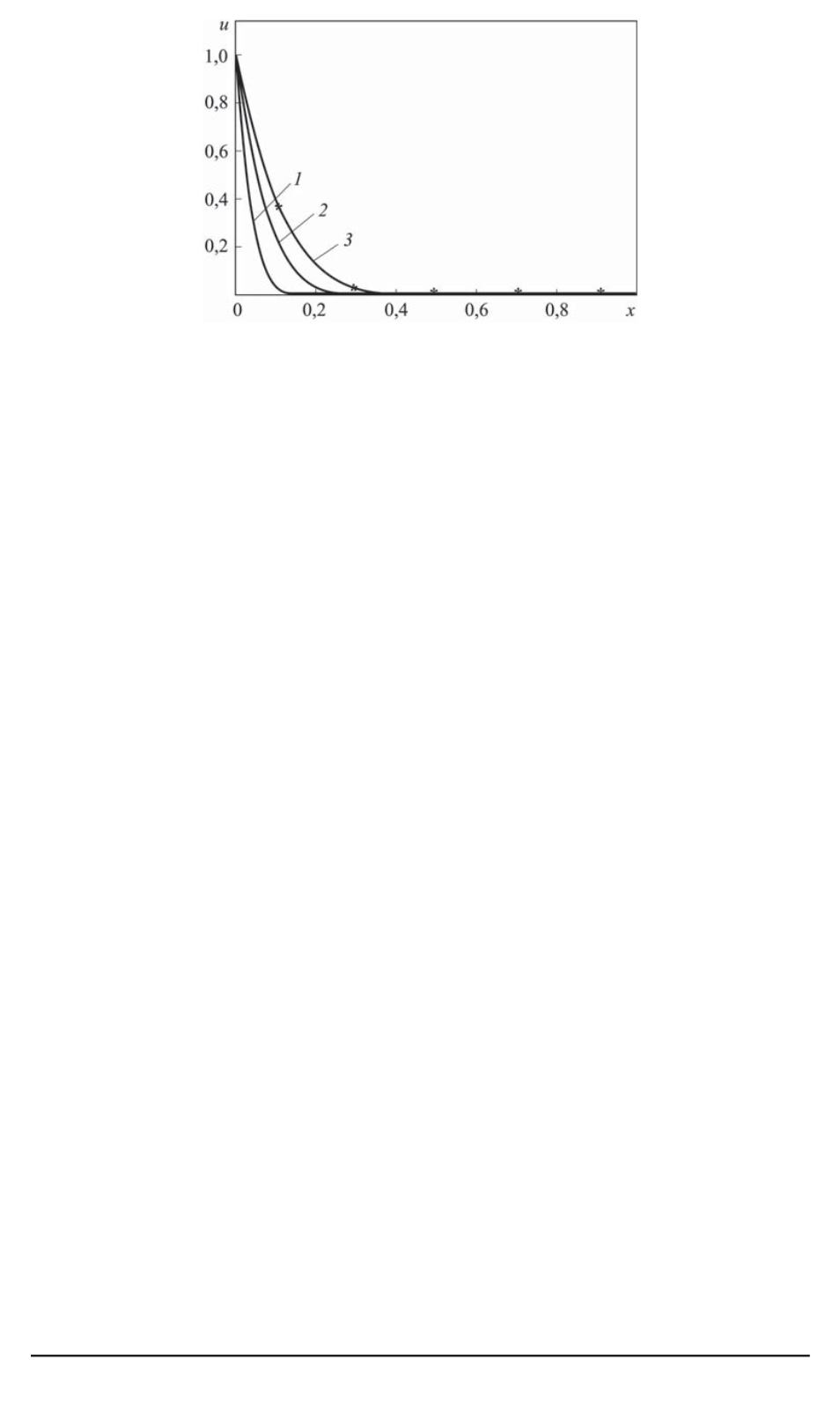
Рис. 4. Распределения температуры в фиксированные моменты времени при
t
1
= 0
,
001
(
1
),
t
2
= 0
,
005
(
2
) и
t
3
= 0
,
1
c (
3
) (–
∗
– — стационарный профиль)
В примере
α
= 1
/
2
<
1
, поэтому наблюдаются все эффекты, кото-
рые были рассмотрены ранее.
Распределения температуры для трех моментов времени приве-
дены на рис. 4. Для этих кривых значения фронтовых точек равны:
x
1
∗
= 0
,
10
;
x
2
∗
= 0
,
37
;
x
3
∗
= 0
,
49
.
Расчеты показали, что при
t > t
3
процесс выходит на стационар-
ный режим
u
st
(
x
) =
(1
−
2
x
)
4
, x <
0
,
5;
0
, x
≥
0
,
5
.
Следует отметить, что значение относительной погрешности прибли-
женного решения при
t
=
t
3
по сравнению со стационарным реше-
нием, не превышает 0,1% и в последующие моменты времени не
увеличивается.
В задаче (10) при
t
→ ∞
тепловое возмущение проникает в слой
на конечную глубину (
L
= 0
,
5
), причем за пределами этой глубины
(
0
,
5
≤
x
≤
1
), температура равна нулю, т.е. тепловое возмущение,
распространяющееся от левой поверхности
x
= 0
, не достигает правой
поверхности
x
= 1
.
Выводы.
Численное решение краевой задачи (1) для квазилиней-
ного параболического уравнения подтверждает теоретический вывод,
что при некоторых значениях параметров в задаче наблюдается эф-
фект пространственной локализации возмущений. При наличии этого
эффекта тепловые возмущения от нагретой поверхности проникают в
слой лишь на конечную глубину даже за неограниченный промежуток
времени.
СПИСОК ЛИТЕРАТУРЫ
1.
Мартинсон Л.К.
,
Малов Ю.И.
Дифференциальные уравнения математической
физики. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 368 с.
2.
Мартинсон Л.К.
Исследование математической модели процесса нелинейной
теплопроводности в средах с объемным поглощением / В кн.: Математическое
моделирование. Процессы в нелинейных средах. М.: Наука, 1986. С. 279–309.
32
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 4


