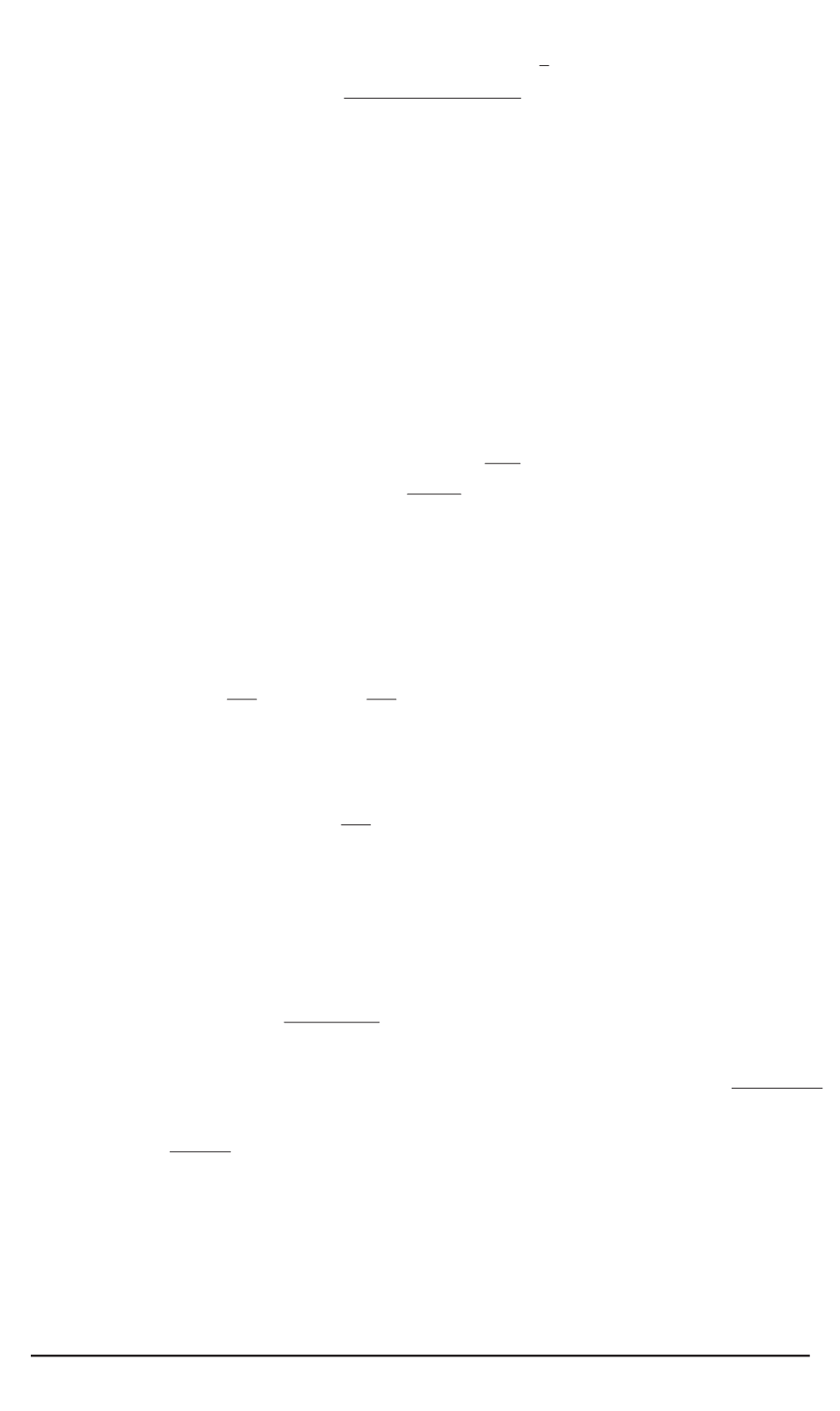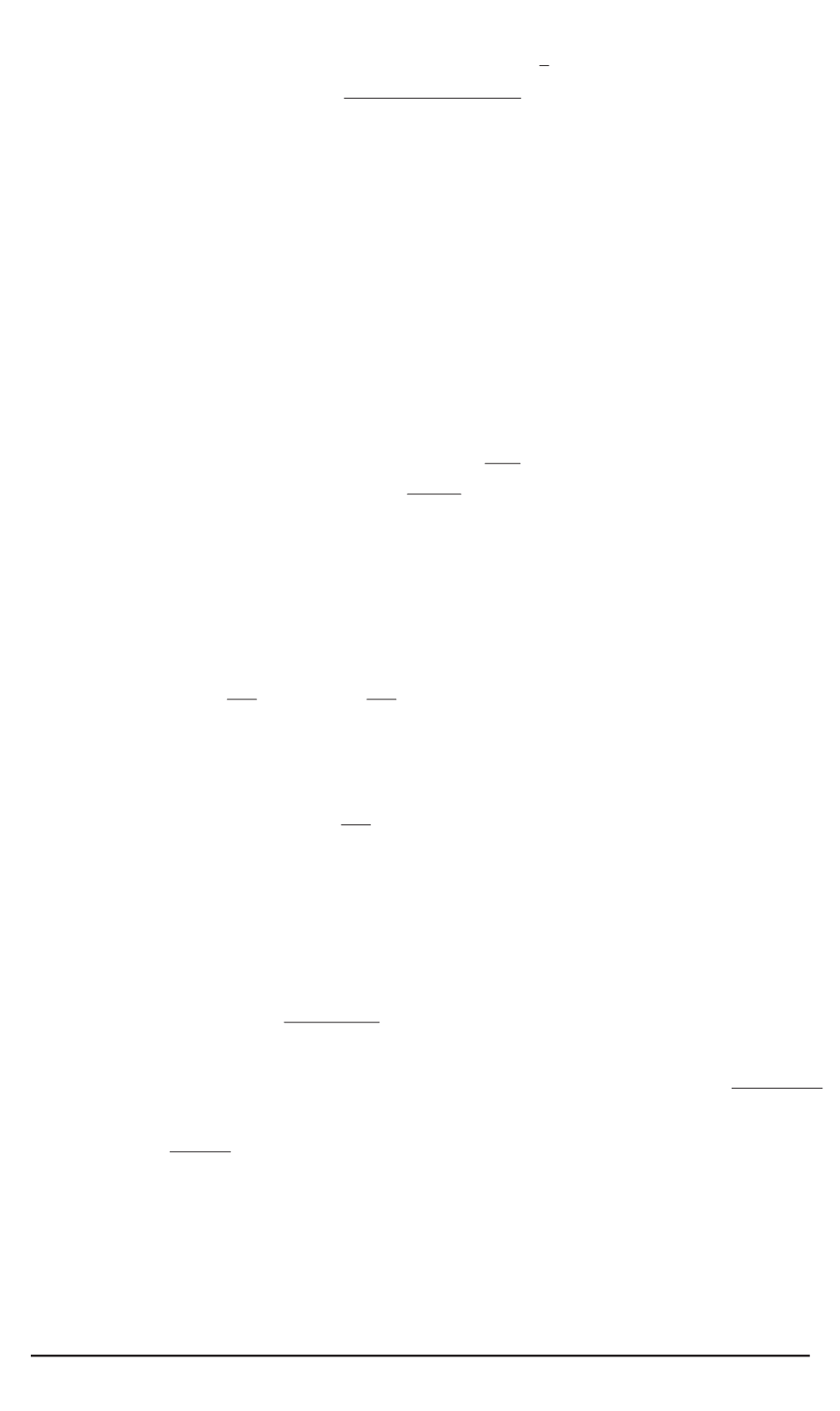
Здесь
L
=
2
U
1
−
α
0
a
2
(1 +
α
)
p
(1
−
α
)
2
1
2
;
(2)
a
2
=
λ/
(
ρc
)
;
p
=
p
0
/
(
ρc
)
.
Далее исследуем задачи, для которых
L < l
, когда в задаче (1)
наблюдается эффект пространственной локализации тепловых возму-
щений.
Согласно теоремам сравнения, приведенным в работе [3], суще-
ствование стационарного решения (2) означает следующее: для лю-
бого
t
∈
[0
,
∞
)
решение задачи (1) мажорируется стационарным ре-
шением, т.е.
u
(
x, t
)
≤
u
st
(
x
)
. Это позволяет записать приближенное
решение задачи (1) в форме тепловой волны с конечной скоростью
перемещения ее фронта
u
(
x, t
) =
⎧⎪⎨ ⎪⎩
U
0
1
−
x
x
∗
(
t
)
2
1
−
α
, x < x
∗
(
t
);
0
, x
≥
x
∗
(
t
)
.
(3)
Для нахождения закона движения фронта тепловой волны запишем
интегральное условие теплового баланса
x
∗
(
t
)
0
∂u
∂t
dx
=
−
a
2
∂u
∂x
x
=0
−
p
x
∗
(
t
)
0
u
α
(
x, t
)
dx,
(4)
в котором учтено условие
∂u
∂x
x
=
x
∗
(
t
)
= 0
,
соответствующее равенству нулю теплового потока на фронте
x
=
x
∗
(
t
)
.
Подставляя предполагаемую форму решения (3) в (4) и вычисляя
интегралы в обеих частях равенства (4), получаем дифференциальное
уравнение
d
(
x
2
∗
(
t
))
dt
=
b
0
−
b
1
x
2
∗
(
t
)
,
(5)
где
b
0
,
b
1
— постоянные, определяемые по выражениям
b
0
= 4
a
2
3
−
α
(1
−
α
)
2
,
b
1
= 2
U
α
−
1
0
p
3
−
α
1 +
α
.
Очевидно, что искомая функция должна удовлетворять начальному
условию
x
∗
(0) = 0
.
(6)
Интегрируя дифференциальное уравнение (5) и учитывая началь-
ное условие (6), находим
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 4
29