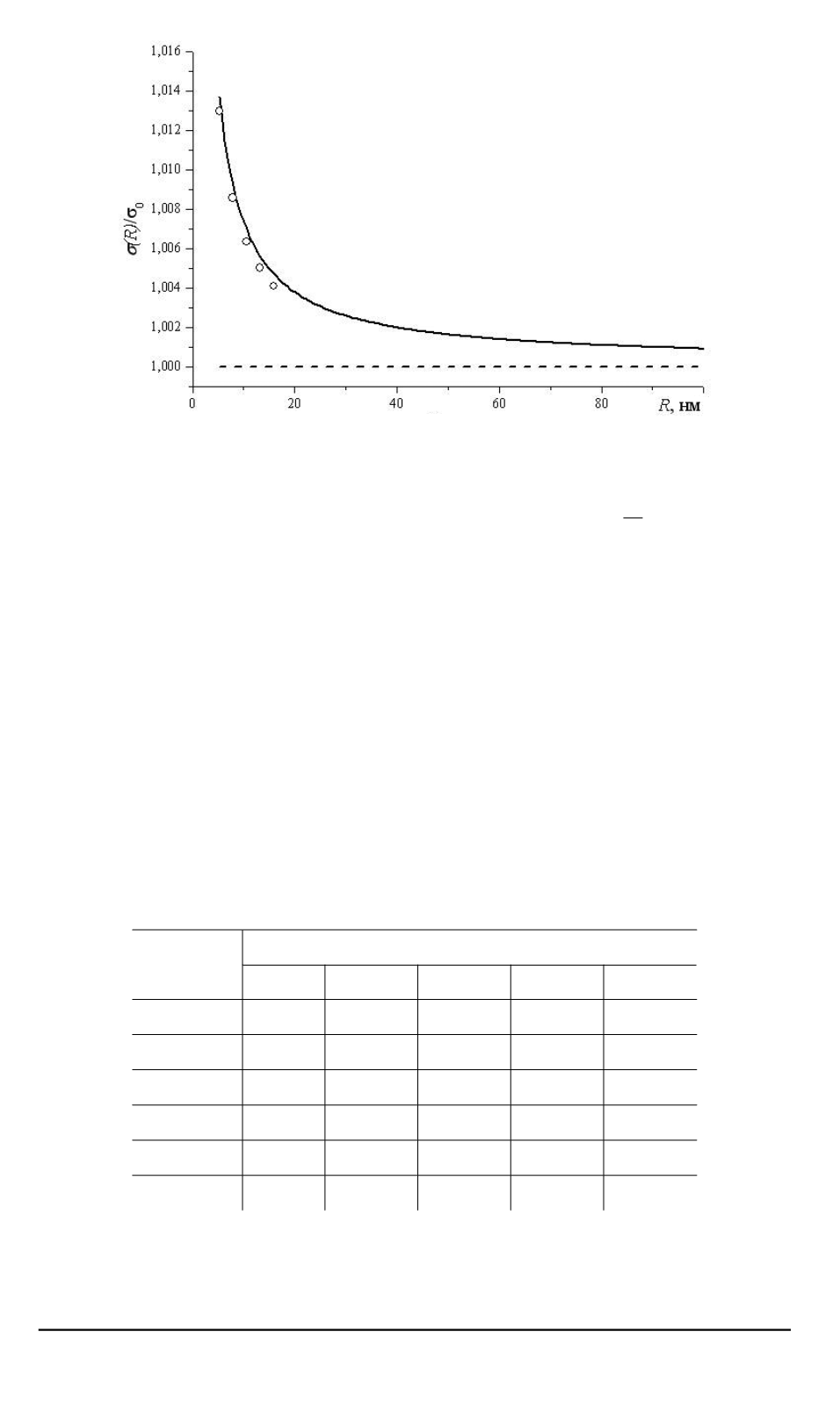
Рис. 1. Зависимость поверхностной энергии сферической частицы алюминия от
радиуса
совпадающему с (2), если вместо
β
в него подставить
a
R
и учесть, что
ln 2
≈
0
,
693
.
На рис. 1 приведен график размерной зависимости поверхностной
энергии сферической частицы алюминия, нормированной на значение
для полубесконечного объема металла. Сплошная линия показывает
значения, рассчитанные по аналитическим формулам (5)–(9), кружка-
ми помечен результат численного интегрирования, штриховые линии
соответствуют значению поверхностной энергии для полубесконечно-
го образца с плоской поверхностью раздела металл–вакуум.
Абсолютные значения оценок поверхностной энергии приведены
в табл. 2.
Таблица 2
Поверхностная энергия металлических частиц при
различных значениях радиуса
σ
(
R
)
, эрг/см
2
R
, нм
K Li
Mg
Pb
Al
1
71
261
473
691
913
5
67
247
449
656
866
10
66
245
445
651
860
50
66
244
443
647
855
100
65
243
442
647
854
∞
65
243
442
646
853
Результаты расчетов показывают, что составляющая поверхност-
ной энергии, связанная с релаксацией электронного облака, растет с
44
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 2


