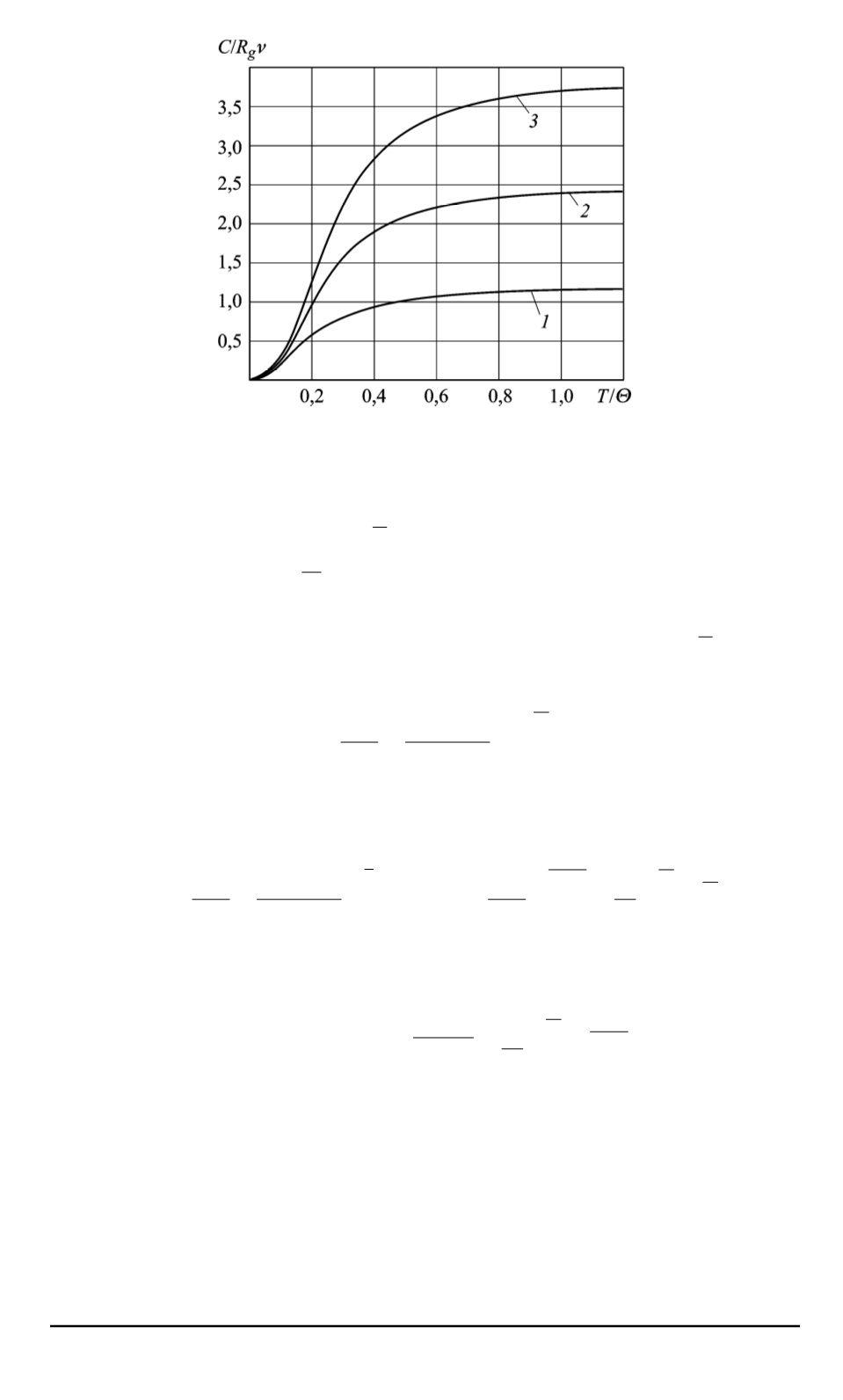
Рис. 3. Зависимость теплоемкости фрактальной структуры (
D
= 2
,
5
) от темпе-
ратуры в случае различной связности:
1, 2, 3
—
θ
=
−
1
,
0
,
1
соответственно
F
=
Nε
0
+
νRTD
2
T
Θ
D
Θ
T
Z
0
z
D
−
1
ln 1
−
e
−
z
dz
=
=
Nε
0
+
νRTD
2
1
Z
0
z
D
−
1
ln 1
−
e
−
Θ
T
z
dz
;
Θ =
~
u
0
k
2
π
2
N
A
ν
V
D
1
D
.
Обобщенная температура Дебая выражается через обычную харак-
теристическую температуру Дебая для 3D-кристаллов как
Θ
0
=
~
u
0
k
6
π
2
N
A
ν
V
1
3
)
Θ =
k
~
u
0
3
−
D
D
D
3
1
D
Θ
3
D
0
и зависит от структуры, так как связана с размерностью; при скорости
звука
u
0
10
3
м/с имеем
Θ = ˜
T
Θ
0
,
˜
T
= 10
8(3
−
D
)
D
D
3
1
D
Θ
3
−
D
D
0
.
Характерный вид функции
˜
Т
приведен на рис. 4. Даже малое
уменьшение фрактальной размерности структуры приводит к суще-
ственному увеличению обобщенной температуры Дебая.
При характерных значениях фрактальной размерности для класте-
ров карбидных материалов обобщенная температура Дебая может от-
личаться от обычной характеристической температуры Дебая в не-
сколько десятков раз.
58
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4


