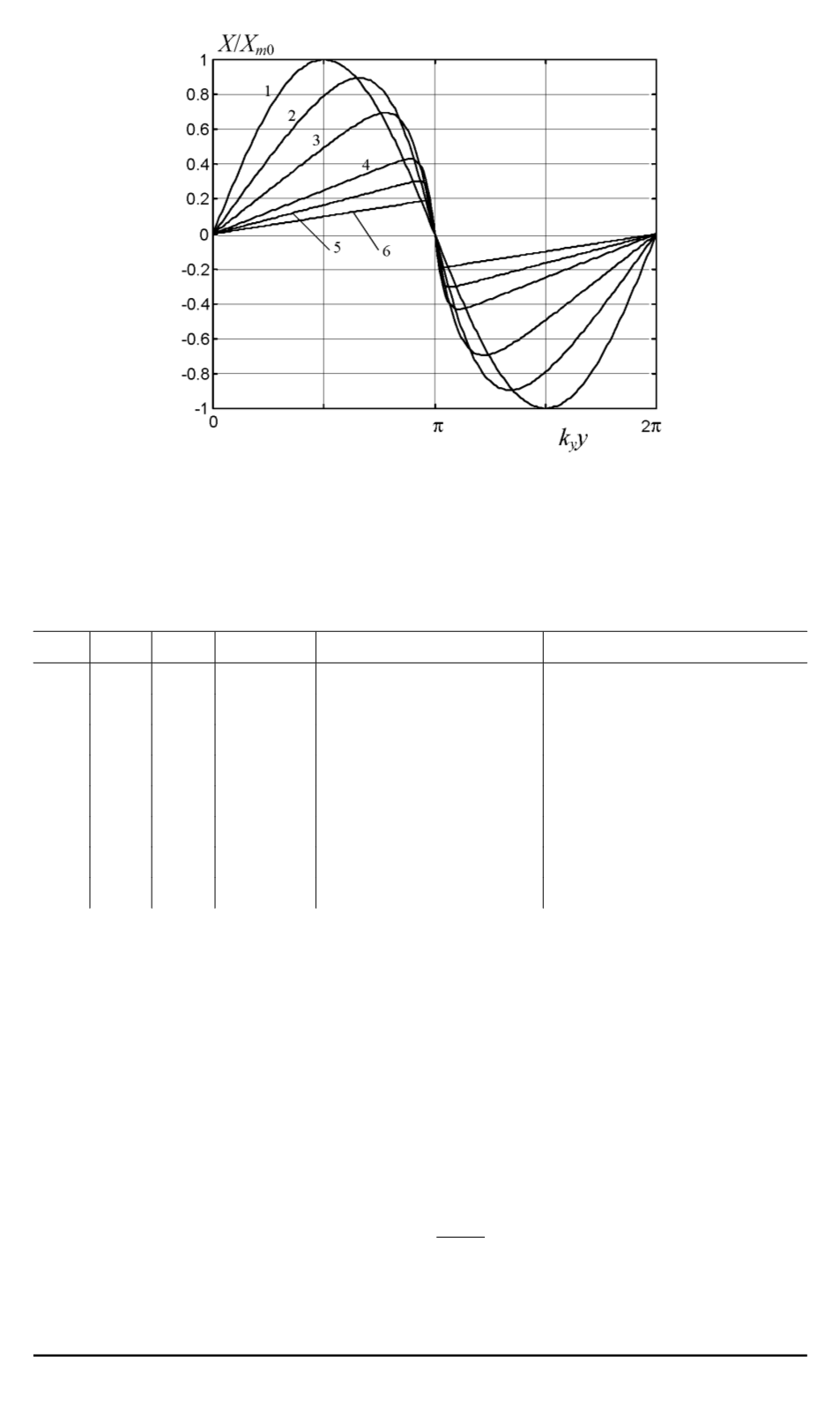
Рис. 3. Стационарные профили волны:
γ
s
/γ
= 0
, 0,5, 1, 2, 3, 5 (соответственно кривые
1, 2, 3, 4, 5, 6
);
D
=
D
Таблица 1
Результаты расчета для различных значений параметра шира
γ
s
при
линейной зависимости скорости ширового течения и
D
=
D
γ
s
/γ γ
0
/γ τ
NL
γ X
2
m
/X
2
m
0
X
2
m
/X
2
m
0
при
D D D
?
/D
?
0
по формуле (5)
0 0 –
1
–
1
0,5 0,090 20 0,80
3,8
0,80
1 0,22 12 0,48
0,96
0,50
1,5 0,31 6,5 0,29
0,43
0,31
2 0,36 5,0 0,18
0,24
0,20
3 0,40 5,0 0,090
0,11
0,10
5 0,44 5,0 0,037
0,038
0,038
10 0,45 5,0 0,0095
0,0098
0,0099
В связи с указанным обстоятельством предположим, что на основе
рассматриваемой модели нелинейной волны можно рассматривать де-
формацию элемента среды под воздействием произвольного ширового
течения, а не только течения с постоянным широм.
Определенный интерес представляет случай квадратичного рас-
пределения скорости течения с экстремумом при
x
=
x
0
. Зададим
зависимость скорости (в размерных единицах) в виде
V
(
x
) =
γ
2
x
2
X
m
0
,
(16)
где
γ
2
— постоянная, имеющая ту же размерность, что
γ
s
и
γ
; в качестве
масштаба
γ
2
используем величину
γ
.
10
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3


