Аналогично уравнению (13) для случая зависимости (16) получаем
уравнение, описывающее профиль волны
∂X
∂t
+
γ
2
X
2
X
m
0
∂X
∂y
=
D
∂
2
X
∂y
2
+
γX.
(17)
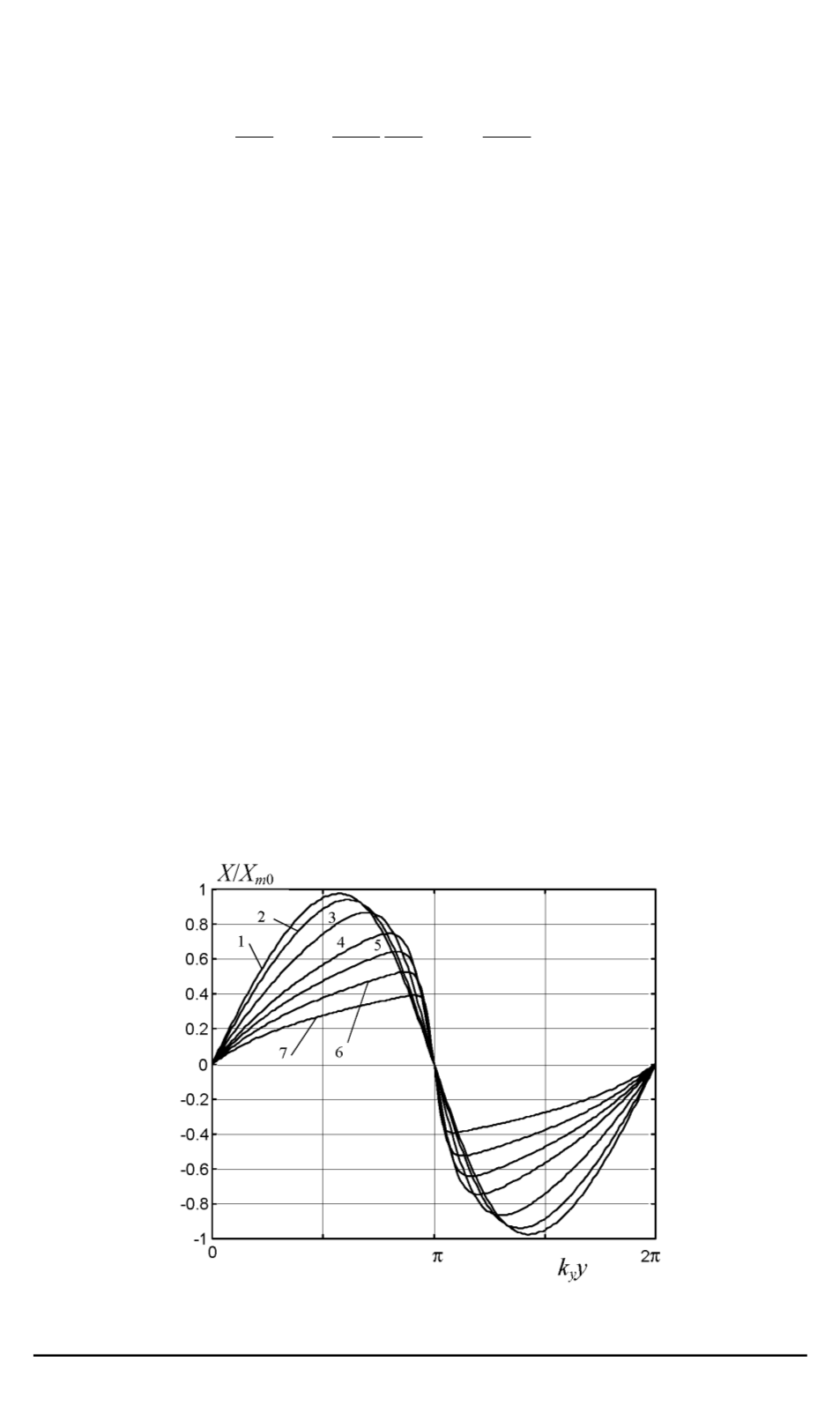
Результаты решения уравнения (17) с теми же начальными и гра-
ничными условиями, что и для (13), приведены на рис. 4–6 и в табл. 2.
В результате расчетов получено, что при
D D
, а также при
D
=
D
и
γ
2
1
эффективный инкремент для начальной волны малой ам-
плитуды
γ
0
≈
0
,
45
, характерное время перехода от линейного роста
амплитуды к насыщению составляет
τ
NL
≈
3
. Для
γ
2
>
2
результаты
расчетов величины
D
с приемлемой точностью можно аппроксими-
ровать зависимостью
D
≈
2
D
0
γ/
|
γ
2
|
.
Обсуждение результатов.
Рассмотрим возможности и ограниче-
ния сформулированной модели применительно к исследованиям ано-
мального транспорта в плазме.
1.
Условия существования нелинейных дрейфовых волн
. Фазовые
скорости и инкременты Фурье-гармоник, на которые может быть раз-
ложена нелинейная волна, должны не сильно изменяться в зависимо-
сти от волнового числа. Тогда за характерное время формирования
стационарного профиля нелинейной волны ее искажение и распад из-
за дисперсии будут несущественны. В результате расчетов было уста-
новлено, что время перехода от линейной стадии роста амплитуды до
насыщения
τ
NL
5
/γ
(в случае линейной зависимости
V
(
x
)
). Эту
величину, видимо, можно рассматривать в качестве масштаба време-
ни формирования стационарного профиля. Тогда дисперсией можно
Рис. 4. Стационарные профили волны:
γ
2
/γ
= 0
,
3
, 0,5, 1, 2, 3, 5, 10 (соответственно кривые
1, 2, 3, 4, 5, 6, 7
);
D
=
D
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3
11


