вектор
k
=
col
(
k
1
, . . . ,
k
n
)
задает точность структурного моделирова-
ния. Очевидно, что
δ
i
(α
x
(
∙
)
,
α
u
(
∙
))
=
δ
i
(
x
(
∙
)
,
u
(
∙
))
,
α
2
R
.
Анализ критерия (6) приводит к следующему заключению: при
выполнении условия
1(
x
(
∙
),
u
(
∙
))
6
=
0
возможна параметрическая
идентифицируемость уравнений МДЭП (здесь термин идентифици-
руемость тождествен понятию единственность). Этот критерий, в
частности, определяет необходимый выбор в процессе идентифика-
ции функционального семейства входных воздействий
{
u
j
(
∙
)
:
u
j
(
∙
)
2
L
2
(
T
),
j
=
1
, . . . ,
m
}
,
где
L
2
(
T
)
— пространство вещественных функций на
T
, суммируемых
с квадратом. В терминах теоремы 2 из работы [6] данное условие опре-
деляется геометрией этого семейства в пространстве
L
2
(
T
)
, а именно:
dim Span
{
u
j
(
∙
)
:
u
j
(
∙
)
2
L
2
(
T
),
j
=
1
, . . . ,
m
} =
m
,
причем проверка последнего равенства легко осуществима, например
с помощью процедуры ортогонализации Грама–Шмидта в простран-
стве
L
2
(
T
)
[3, с. 30].
Из анализа формулы (7) следует, что в условиях приближенно-
го моделирования (см. ранее рассмотренный критерий
δ
i
(
x
(
∙
),
u
(
∙
))
,
i
=
1
, . . . ,
n
для выбора структуры МДЭП) равенство (7) — есть ре-
шение задачи параметрической оптимизации вида
min
Z
T
(
||
dx
(
t
)/
dt
−
Ax
(
t
)
−
Bu
(
t
)
||
R
n
)
2
dt
,
где
|| ∙ ||
R
n
— евклидова норма в
R
n
.
Программная среда “РЕДИМ”. Анализ результатов моделиро-
вания.
Для решения означенного выше круга задач апостериорного
моделирования динамики процесса гальванизации был использован
программный комплекс “РЕДИМ” (реализация динамической моде-
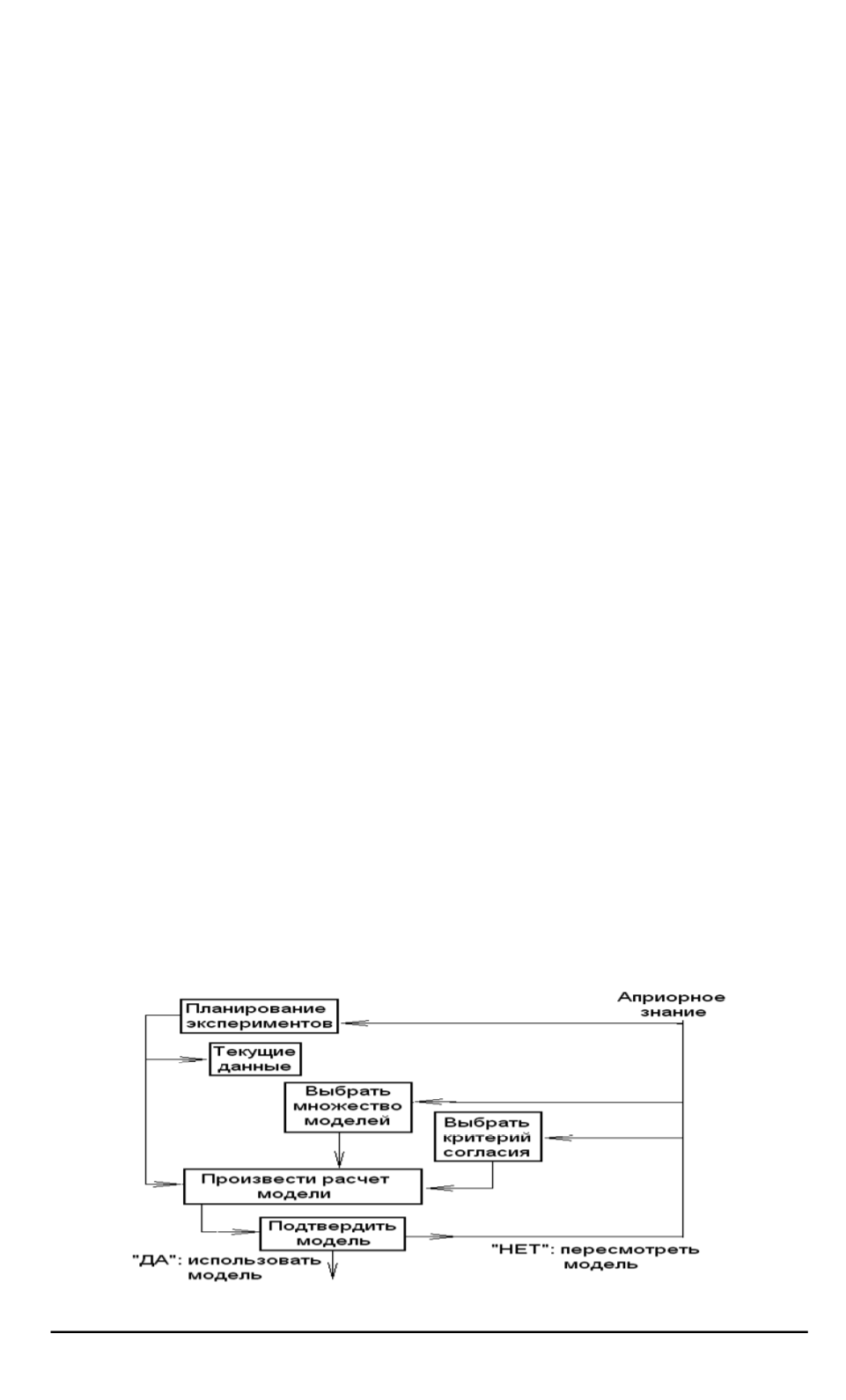
Рис. 1. Схема принятия решений, реализованная в пакете “РЕДИМ”
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4
101


