коэффициентов для терминальных ограничений до приближенного
выполнения ограничений в конечный момент времени. На заключи-
тельном этапе минимизировали суммарный функционал
s
0
J
(
u
)
+
+
(
1
−
s
0
)
I
(
x
)
, что, по существу, позволило уточнить приближенно-
оптимальное управление. Резюмируя моделирование ОРЭП в целом,
отметим, что на его первых этапах применялись методы градиентного
типа, на последнем — методы второго порядка; результаты расчетов
приведены на рис. 6–10.
Анализ результатов численного моделирования показал, что ОРЭП-
технология для нестационарного режима цинк-железной гальванооб-
работки позволяет осуществить экономию в виде ресурсосбережения,
выраженного через функционал затрат (10), относительно исходной
МДЭП-технологии на 150%.
Выводы.
1. Для комплексного исследования апостериорной мате-
матической модели процесса электроосаждения цинк-железного спла-
ва в условиях управляемых режимов обновления электролита и вра-
щения анода привлечен аппарат теории реализации динамических си-
стем в классе линейных стационарных дифференциальных уравнений
с программным управлением. Определена репрезентативная диффе-
ренциальная модель управляемой динамики процесса гальванизации.
Установлено хорошее совпадение этой модели с экспериментальными
данными.
2. Поставлена и исследована задача оптимизации режима галь-
ванизации, сберегающего энергетические и материальные затраты.
Для различных вариантов граничных условий электролиза разработа-
на алгоритмическая ОРЭП-технология оптимизации нестационарного
электролитического процесса, представляющая собой цепь конечных
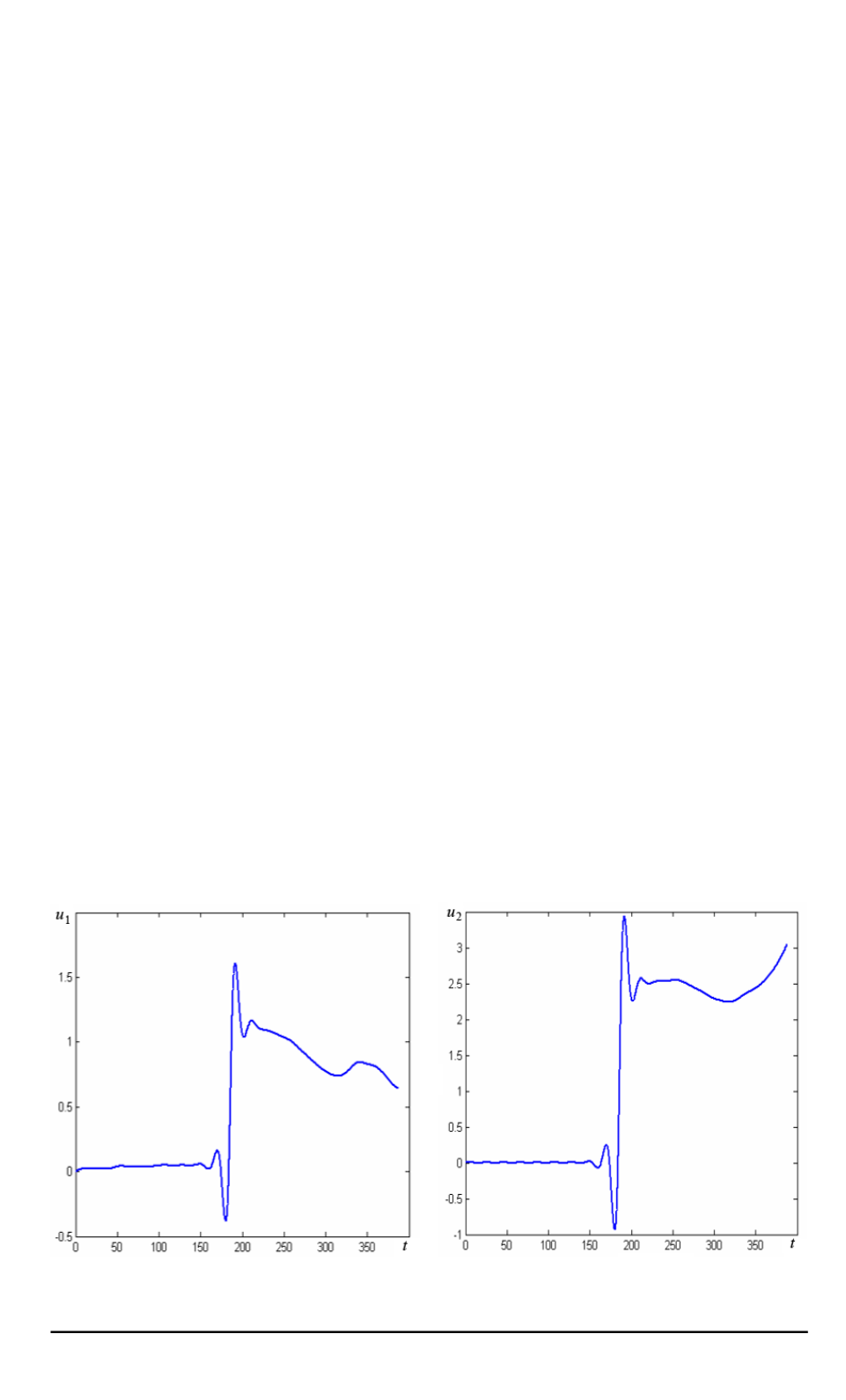
Рис. 6. Оптимальная программа катод-
ной плотности электротока
u
1
опт
(
t
)
Рис. 7. Оптимальная программа скоро-
сти протока электролита
u
2
опт
(
t
)
106
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4


